P4072[SDOI]2016征途

我走过万水千山，邂逅了无数美丽与丑陋的灵魂，只为寻找一个留在这个世界上的理由。

原题题面

题目描述

Pine 开始了从 $S$ 地到 $T$ 地的征途。

从 $S$ 地到 $T$ 地的路可以划分成 $n$ 段，相邻两段路的分界点设有休息站。

Pine 计划用 $m$ 天到达 $T$ 地。除第 $m$ 天外，每一天晚上 Pine 都必须在休息站过夜。所以，一段路必须在同一天中走完。

Pine 希望每一天走的路长度尽可能相近，所以他希望每一天走的路的长度的方差尽可能小。

帮助 Pine 求出最小方差是多少。

设方差是 $v$，可以证明，$v×m^2$ 是一个整数。为了避免精度误差，输出结果时输出 $v×m^2$。

题目大意

给出 $n$ 个数$a_1,a_2,\cdots,a_n$，你可以将其恰好分成连续的 $m$ 段，使得这 $m$ 段的和的方差最小。

输入

第 $1$ 行两个正整数 $n,m$
第 $2$ 行 $n$ 个正整数 $a_1,a_2,\cdots,a_n$

输出

$1$ 行 $1$ 个整数，代表最小的方差与 $m^2$ 的乘积（可以证明，此时答案一定是整数）

数据范围

$1 \le n \le 3000, 1\le m \le n, \sum a_i \le 3\times 10^4$

题解部分

前置工作

首先，经典套路拆方差：
记 $x_i$ 为划分出来第 $i$ 段的和，

$$ S^2 = \frac1m\sum_{i=1}^{m}(x_i-\bar{x})^2 $$

$$ m^2\cdot S^2 = m\cdot \sum_{i=1}^{m}(x_i-\bar{x})^2 $$

$$ = m\cdot \sum_{i=1}^{m}(x_i^2+\bar{x}^2-2x_i\bar{x}) $$

$$ = m\cdot \sum_{i=1}^{m}x_i^2 + m\cdot \sum_{i=1}^{m}\bar{x}^2 - 2m\cdot \sum_{i=1}^{m}x_i\bar{x} $$

$$ = m\cdot \sum_{i=1}^{m}x_i^2 + m\bar{x}^2\cdot \sum_{i=1}^{m}1 - 2m\bar{x}\cdot \sum_{i=1}^{m}x_i $$

$$ = m\cdot \sum_{i=1}^{m}x_i^2 - (\sum_{i=1}^{m}x_i)^2 $$

此式第二项为定值可预处理，要求第一项最小，即要求平方和最小。

可以写出一个裸DP：
首先求好前缀和 $s$，
设 $dp_{i,j}$ 表示目前划分到第 $i$ 段，这一段以 $j$ 结尾的最小平方和，

$$ dp_{i,j} = \min_{k<j}\{dp_{i-1,k}+(s_j-s_k)^2\} $$

枚举上一段的结尾，即可转移，复杂度$O(mn^2)$

复杂度错误，考虑优化。

斜率优化

一旦看起来没有状态浪费的DP复杂度错了，其中一定有隐藏的特性来保证复杂度。

展开：

$$ dp_{i,j} = \min_{k<j}\{dp_{i-1,k}+s_j^2+s_k^2-2s_js_k\} $$

因为状态复杂度看起来没有浪费，我们希望去掉转移枚举的复杂度。

我们枚举了 $i,j$ ，那么 $i,j$ 就是定值。现在我们希望不枚举 $k$ 来保证复杂度。

那我们就需要观察一下哪些前继状态是可能对答案有贡献的。

$$ dp_{i-1,k} - s_k^2 = 2s_js_k + dp_{i,j} - s_j^2 $$

把上式拆开左右移项，得到这个式子。由于把 $\min$ 的限制取消了，这里每个 $k$ 都能使方程解出一个 $dp_{i,j}$ ，我们依旧是希望找到一个 $k$ 使得 $dp_{i,j}$ 最小。

接下来是斜率优化经典转换。

我们找到式中与 $k$ 相关的两项，他们都是给出一个 $k$ 能确定的，这两项我们分别记为 $x_k,y_k$ ：

$$ x_k = s_k $$

$$ y_k = dp_{i-1,k} - s_k^2 $$

那么每个 $k$ 包含与转移有关的信息量都可以用平面直角坐标系上的一个点表示。

接下来我们再观察 $dp_{i,j}$ 能表示成什么。

$$ 2s_j = w $$

$$ dp_{i,j} - s_j^2 = b $$

我们发现原方程变成了

$$ y_k = wx_k + b $$

其中 $w$ 是固定的常量， $b$ 是未知量，要根据另外三个两确定的。

我们要最小化 $dp_{i,j}$，也就是要最小化 $b$ 。

换言之，在平面直角坐标系上，我们枚举完 $i,j$ 后，用一个固定斜率的直线，尝试经过每一个前继状态代表的点 $x_k,y_k$ ，找到一个点能使得截距 $b$ 最小。

画一下：

pFNLOoV.png
pFNLOoV.png

多动一动直线看看，发现只有最外圈凸包上的点才有可能对答案产生贡献：

pFNLzz4.png
pFNLzz4.png

要证明也很简单：

如果一个点是可能对答案有贡献的点，即可能有某一斜率的直线需要取这个点才能使截距最小，那么那条斜线过这个点时，除了这个点在这个直线上，其他的点都需要在这个上侧。

这正好是 “凸” 的定义。

  1. 凸多边形：延长多边形的任意一边为一条直线，若其余的边都在该直线同侧，则称之为凸多边形。——百度百科

那我们只要维护这个凸包就好了。

先考虑加点

如果加入一个点后，这个点完美的融入凸包，那就不需要任何调整：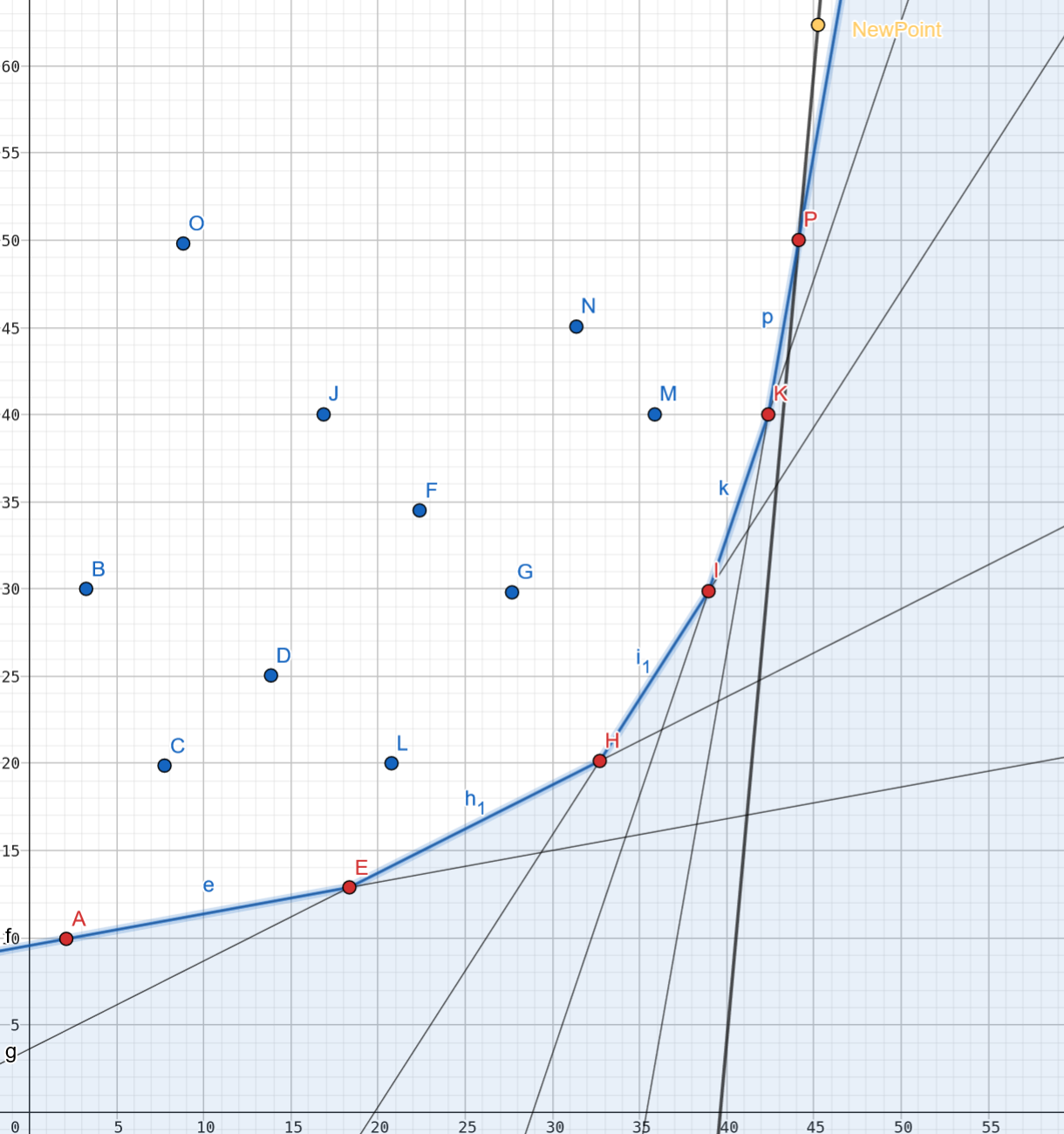

pFNOFdx.png
pFNOFdx.png

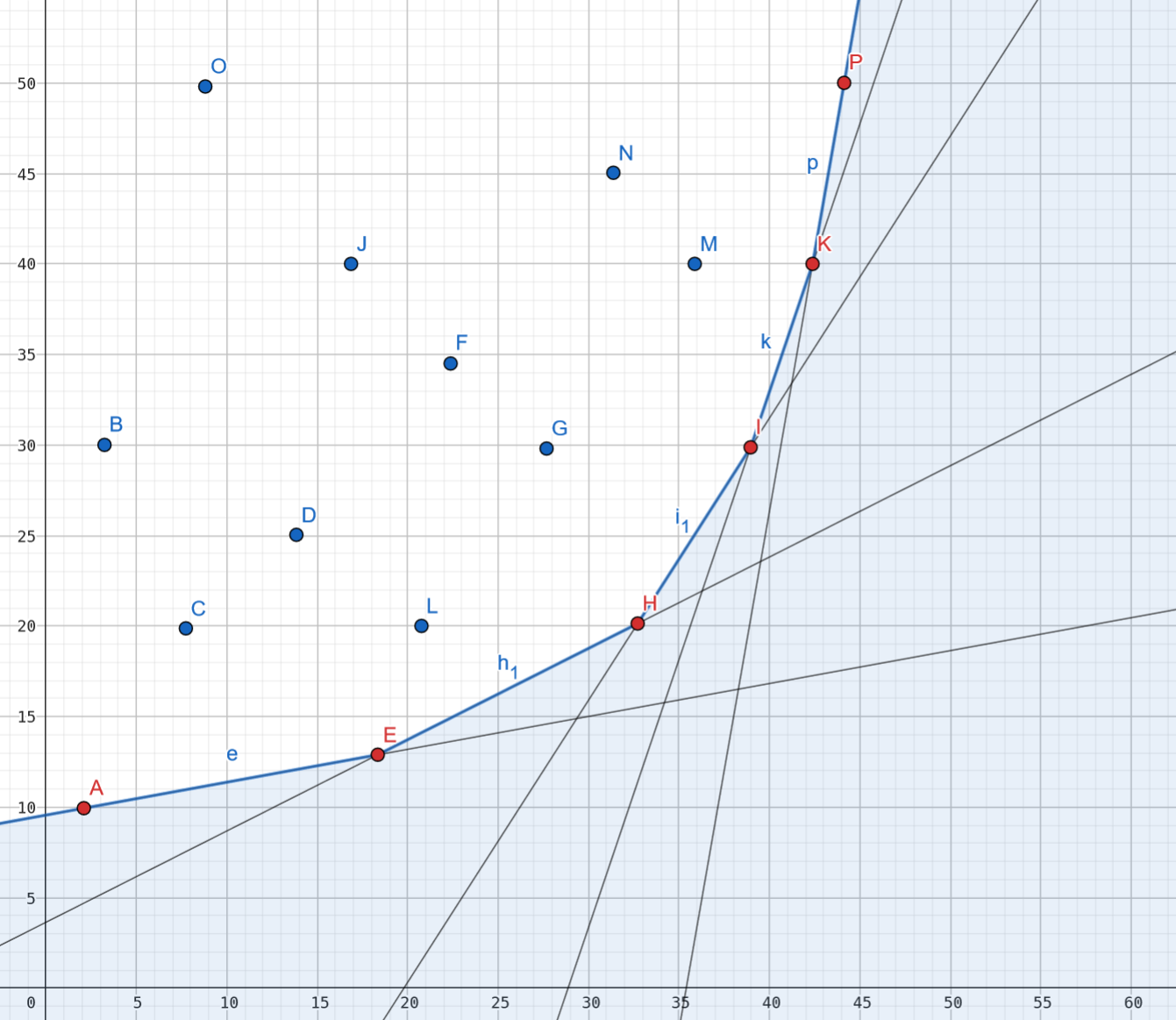
那如果加入凸包后凸包的下凸性质就不成立了呢？

那就从后往前删点，直到剩余图形满足凸包的下凸性质：

0015_1.gif
0015_1.gif

就像这样。

于是我们现在完成了维护凸包的任务。

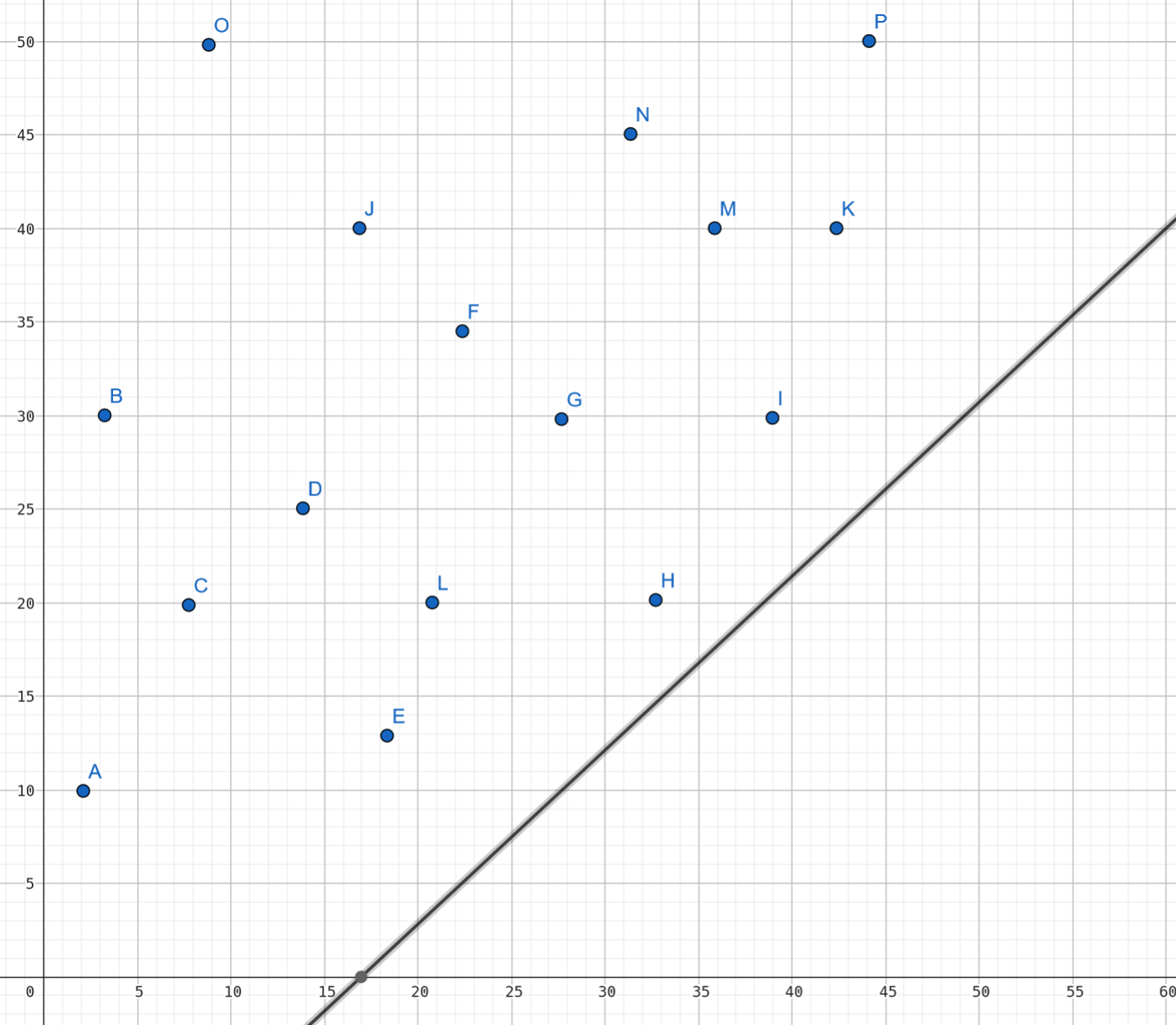
然后考虑截斜线

我们发现一个性质，随着 $j$ 的增大，$s_j$ 是单增的（前缀和啊）。

那么斜率 $w$ 就是单调递增的。

这里的单调能保证什么呢？

如果某个点对答案产生了贡献，由于之后的直线斜率越来越大，这个点左边的点就再也不可能对答案产生贡献了。

所以我们找某个斜率的最优点的时候，甚至不用二分斜率的位置，我们可以直接从最左边删起，直到删到最优点，利用单调性保证复杂度。

0016.gif
0016.gif

就非常好啊，这样我们就可以用单调队列来维护了。由于每层的每个点只会最多被加一次，删一次，所以单层复杂度为 $O(2n)$，所有层的复杂度为 $O(2mn)$

代码实现也很优雅：

#include<bits/stdc++.h>
#define int long long
#define PII pair<int,int>
using namespace std;
const int N = 3005;
int n,m;
int a[N],s[N];
int dp[N][N];
double slope(PII p1,PII p2){//斜率计算
    return (double)(p1.second-p2.second)/(p1.first-p2.first);
}
PII q[N];
signed main(){
    cin>>n>>m;
    memset(dp,0x3f,sizeof(dp));
    dp[0][0]=0;
    for(int i=1;i<=n;i++)cin>>a[i],s[i] = s[i-1]+a[i];
    int h,t;
    for(int i=1;i<=m;i++){
        h=1,t=0;//清空队列
        for(int j=i;j<=n;j++){
            //凸包加点
            PII new_point = {s[j-1],dp[i-1][j-1] + s[j-1]*s[j-1]};
            while(t-h>=1 && slope(q[t],new_point) < slope(q[t-1],q[t]))t--;
            q[++t] = new_point;
            //斜线来截
            int k = 2*s[j];
            while(t-h>=1 && slope(q[h],q[h+1]) < k)h++;
                        
            auto [sk,y] = q[h];//c++17神奇语法
            dp[i][j] = y + s[j]*s[j] - k*sk;
        }
    }
    cout<<m*dp[m][n] - s[n]*s[n];
    return 0;
}