带修莫队复杂度：

$$ O(n^{\frac53}) $$

普通莫队+树状数组做带修复杂度：

$$ O((n\log{n})^{\frac32}) $$

图一目了然：$x<10^5,y<10^8$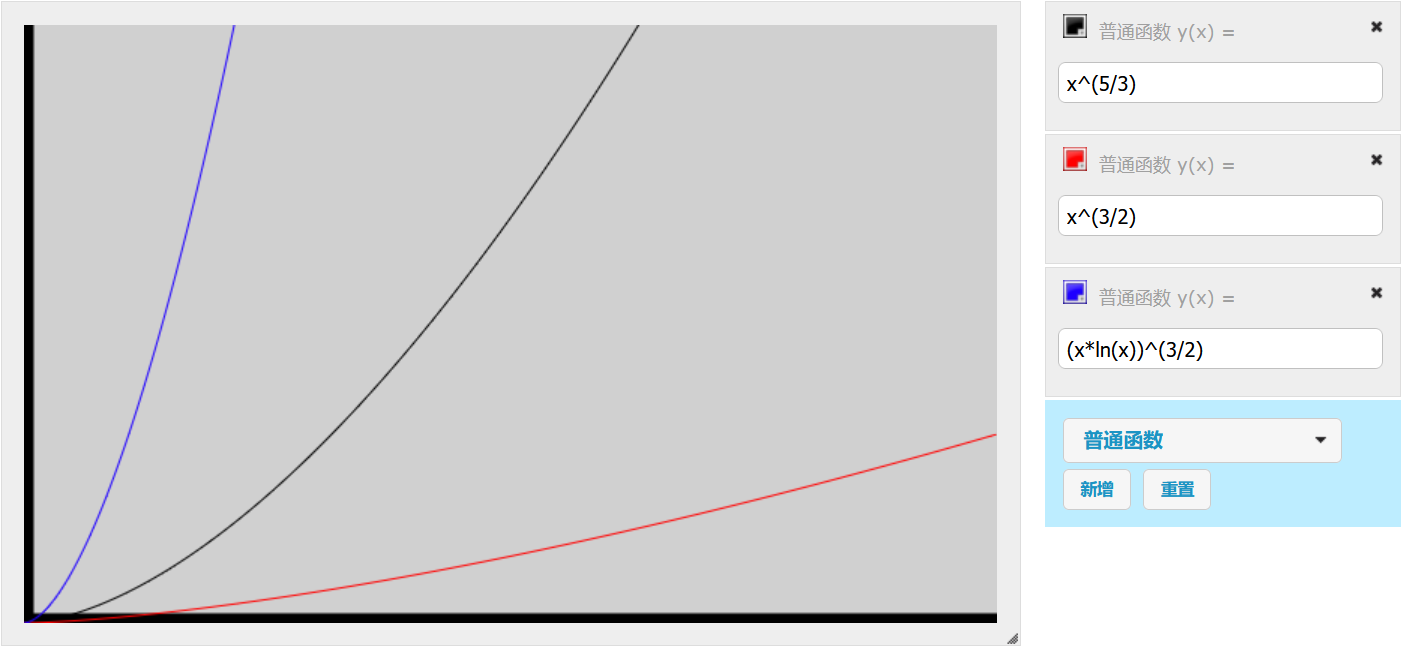

2024-07-08T06:45:16.png
2024-07-08T06:45:16.png

正题（普通莫队-带修莫队）

一般来说，对于一维上区间询问的问题，如果可以离线，就有机会莫队。

要求：

  1. 能离线下来，不能强制在线
  2. 知道某一区间的答案后能 $O(1)$ 求出与之相邻的区间的答案
对于相邻的区间我们这么定义：
记$A=[l_1,r_1],B=[l_2,r_2]$,
我们称 $A$ 与 $B$ 为相邻的区间当且仅当 $|l_1-l_2|+|r_1-r_2|=1$

普通莫队——只有询问，没有修改

莫队算法的精髓在于它处理询问的顺序。

首先，我们可以把区间转化到二维平面上的点，那么相邻的区间在平面上就变成了相邻的格点。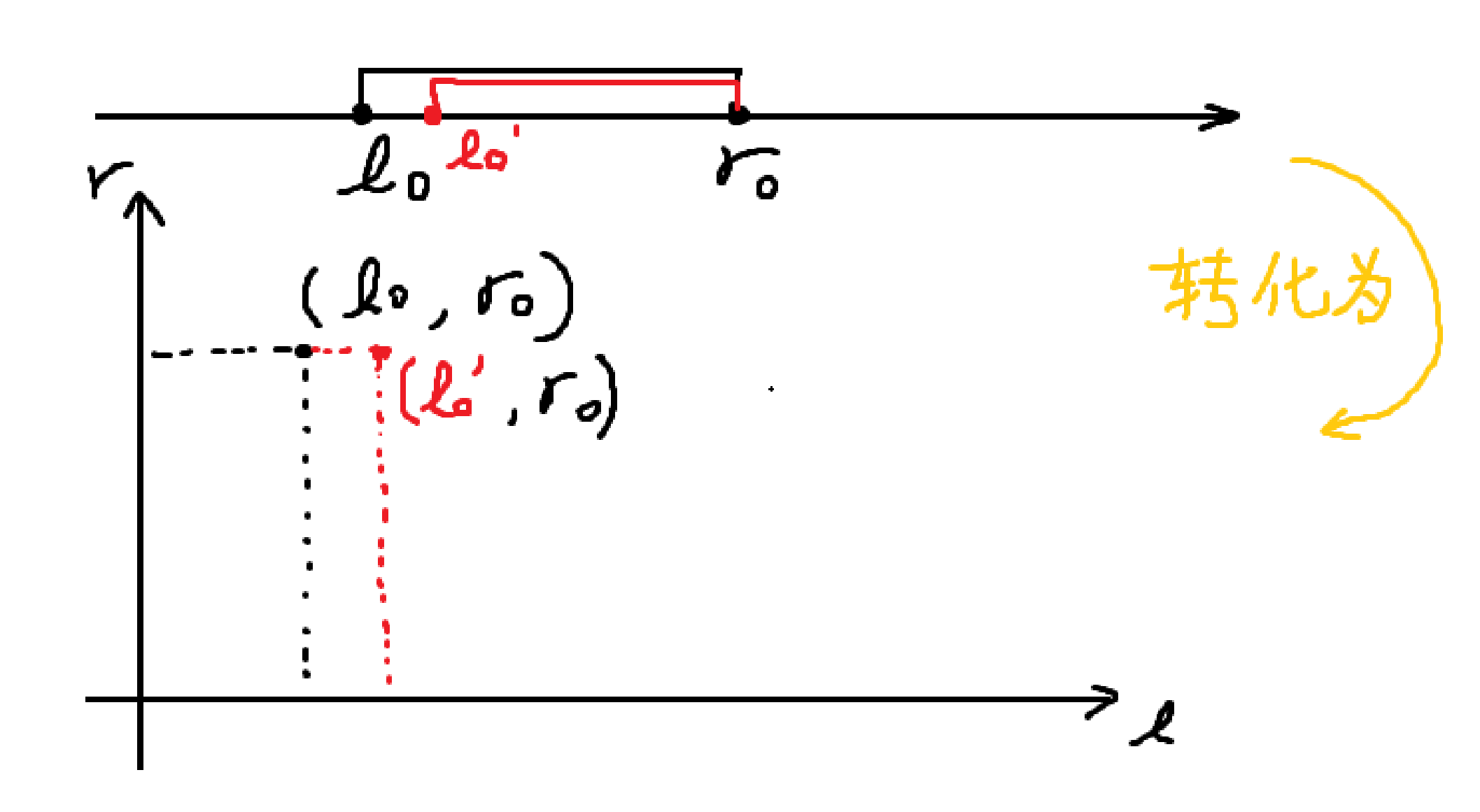

2024-07-08T09:05:11.png
2024-07-08T09:05:11.png

那么从一个区间转移到另一个区间的代价就是这两个区间所代表点在二维平面上的曼哈顿距离。

要在二维平面上走遍所有点的最短路径应当是曼哈顿生成树。
但这东西挺难写得快

于是有了莫队的处理方法：

分块。

把整个长度为 $n$ 的区间分成 $\left \lceil \frac{n}{s} \right \rceil $ 个长度为 $s$ 的不相交区间，称作块。
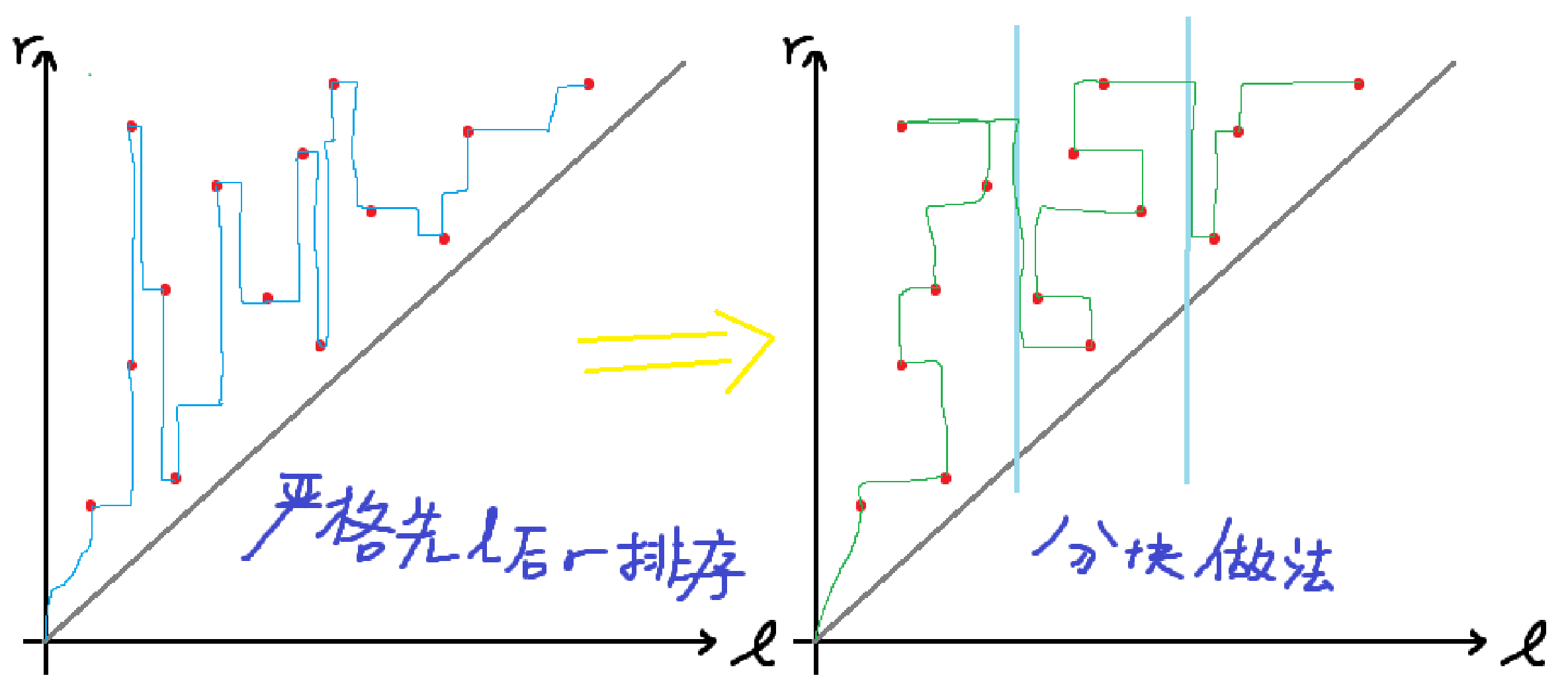
对于询问这样排序：以左端点所在块位置为第一关键字，以右端点位置为第二关键字。
然后跑莫队：从一个询问区间到下一个询问区间，通过不断移动左右端点来实现

复杂度计算：

我们把左端点和右端点移动的复杂度分开来算。

通过上述排序，我们发现询问在大局上是左端点螺旋上升的，局部的块内则是右端点单调递增的。

对于左端点：
在同一块内的每一次移动最多移动块长的距离，$O(s)$，一共 $q$ 次询问，有不超过 $q$ 次这样的移动，$O(qs)$。
在块间的移动一次最多移动 $n$ 的距离，一共移动不超过块数 $\left \lceil \frac{n}{s} \right \rceil $ 次，$O(n\left \lceil \frac{n}{s} \right \rceil )$
对于右端点：
在同一块内由于 $r$ 是单调的，一个块内一共最多移动 $n$ 次，总共 $\left \lceil \frac{n}{s} \right \rceil $ 次，$O(n\left \lceil \frac{n}{s} \right \rceil )$。
在块间的移动一次最多移动 $n$ 的距离，一共移动不超过块数 $\left \lceil \frac{n}{s} \right \rceil $ 次，$O(n\left \lceil \frac{n}{s} \right \rceil )$。

在随机数据下，我们直接把总复杂度记为 $O(\frac{n^2}{s}+qs)$，在 $n$，$q$ 同阶时等于 $O(n(\frac{n}{s}+s))$。

$s$ 是我们自己设置的，显然，这里有均值不等式 $\frac{n}{s}+s \ge 2\sqrt{n}$，

于是，设置恰当的 $s$ ，如 $\sqrt{n}$，可使复杂度达到 $O(n\sqrt{n})$。

分析完毕。

形象化理解：

2024-07-08T09:55:54.png
2024-07-08T09:55:54.png

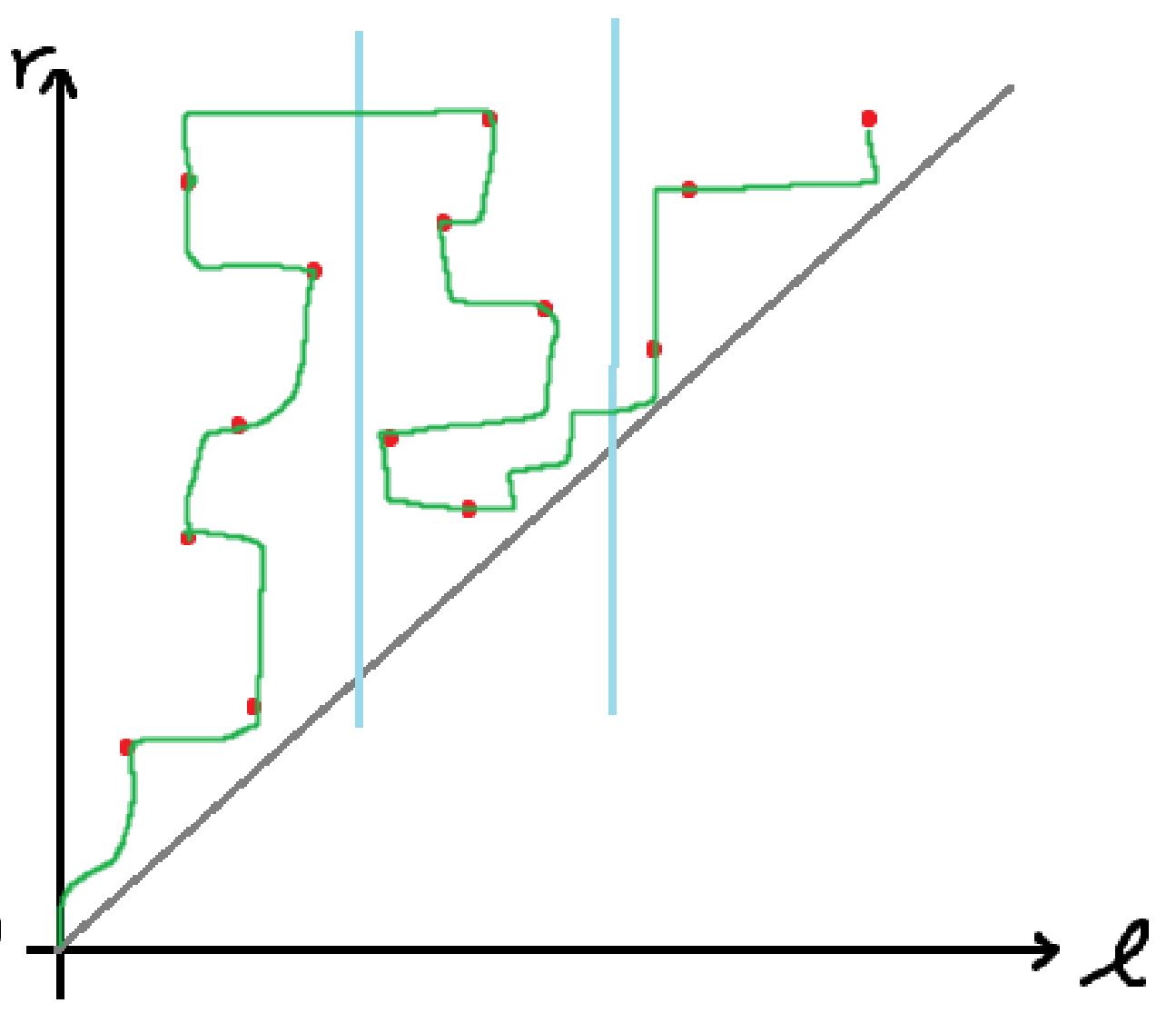
至此，我们还发现分块的右端点做法在块间移动时要返程好一大段，那我们为什么不让它直接倒着回来计算答案呢？
像这样：

2024-07-08T09:59:41.png
2024-07-08T09:59:41.png

此叫做奇偶化排序。对右端点排序时先观察一下左端点所在块的下标的奇偶性，能减少相当的常数。

代码(from oi-wiki)：

void move(int pos, int sign) {
  // update nowAns
}

void solve() {
  BLOCK_SIZE = int(ceil(pow(n, 0.5)));
  sort(querys, querys + m);
  for (int i = 0; i < m; ++i) {
    const query &q = querys[i];
    while (l > q.l) move(--l, 1);
    while (r < q.r) move(++r, 1);
    while (l < q.l) move(l++, -1);
    while (r > q.r) move(r--, -1);
    ans[q.id] = nowAns;
  }
}

带修莫队——有询问，有修改

一种方法，时间维度用树状数组处理掉

复杂度 $O(n\sqrt{n}\log{n})$

由头图得这个东西复杂度堪比 $O(n^2)$

我们换个思路，把它作为第三维，和左右端点同等看待，一起莫队。

就像这个样子：

for(int i=0;i<tot;i++){
    while(l>q[i].l)add(a[--l]);
    while(l<q[i].l)del(a[l++]);
    while(r<q[i].r)add(a[++r]);
    while(r>q[i].r)del(a[r--]);
    while(t<q[i].t)upd(i,++t);
    while(t>q[i].t)upd(i,t--);
    ans[q[i].id] = now;
}

可见莫队算法本身都长一个样，就是排序这一步有所不同。
这里以左端点所在块为第一关键字，右端点所在块为第二关键字，时间为第三关键字。
代码如下：

bool operator<(const nod &x)const{
    if(bl(l)==bl(x.l) && bl(r)==bl(x.r) && (bl(l)&1)==(bl(r)&1))return t<x.t;
    else if(bl(l)==bl(x.l) && bl(r)==bl(x.r))return t>x.t;
    else if(bl(l)==bl(x.l))return bl(r)<bl(x.r);
    else return bl(l)<bl(x.l);
}

现在看来，，只剩证明复杂度的正确性了。

依旧设块长为 $s$，把 $n$，$q$，$t$看作同阶的。

左右端点各自依旧是 $O(ns)$ 级别的
时间维在一个块内是 $O(n)$ 的，一共 $O(\left \lceil \frac{n}{s} \right \rceil^2)$个块，总共$O(\frac{n^3}{s^2})$
总时间复杂度 $O(ns + \frac{n^3}{s^2}) = O(n(s + \frac{n^2}{s^2}))$

求导得 $O(s^3) = O(n^2)$ 时上式取最值。即块长取 $n^{\frac23}$时，此时带回算得总复杂度为 $O(n^{\frac53})$ 。

没啥了，讲的不清楚请cue我。