远处跃动的浮光,朦胧的,遥不可及——
但它一直在那里。
256GaussianPrimeNumber.txt
Encoded.bin
main.exe
puzzle.wav
Readme.mdPart Ⅰ
Hello.
This is a console game.
Your goal is to find the key to decode the encoded data in "Encoded.bin" .
Have fun!
Hint: The next puzzle hides in the final content.main.exe 要求输入13个十位整数。
目标很明确,要解出这个谜题必须要找到13个十位整数。
Part Ⅱ
我们查看 256GaussianPrimeNumber.txt 发现文件中包含用空格分隔的544个质数。
文件名指出:256GaussianPrimeNumber
根据高斯素数的定义:
如果一个整数 $n$ 不能被分解为高斯整数相乘,那么 $n$ 为高斯素数
而利用费马平方和定理
奇质数能表示为两个平方数之和的充分必要条件是该质数被4除余1
这样我们可以通过 p%4==3 来判断判断一个数是否为高斯素数。
with open("256GaussianPrimeNumber.txt", "r") as f:
primes = f.read()
primes = [int(i) for i in primes.strip().split(" ") if int(i)%4==3]我们得到了文件中所有高斯素数。
>>> print(len(primes))
256恰好与文件名描述的一致,接下来的解密需要围绕这256个素数展开。
Part Ⅲ
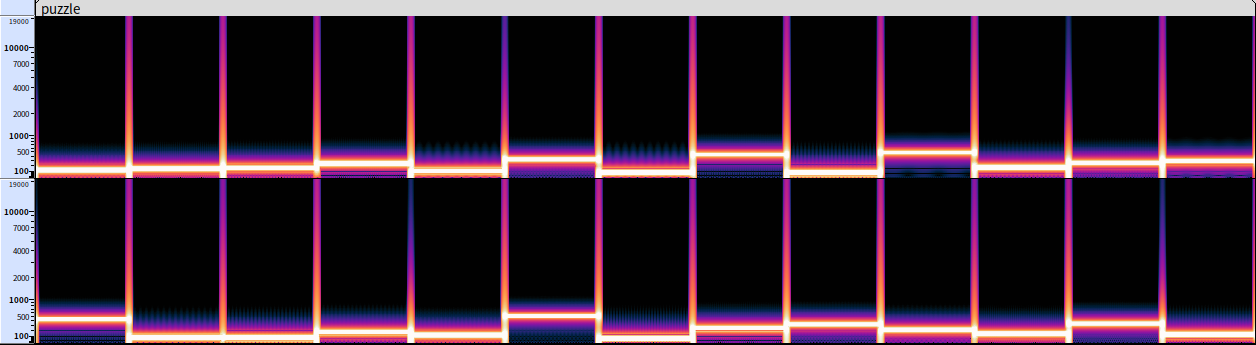
观察wav频谱,发现恰好有13段,双声道,推测一段对应一个整数。
考虑到前面解密内容一直和数字有关,提取每一段的频率试试?
第一段:
124
440
第二段:
147
...这些频率有什么特点?观察可以发现:
- 部分频率数值有重复
- 基本在 100-500 左右
我们发现第一段有一个440,这是什么呢?
音高与频率对照表
我们看第一段第二个频率:440
这是什么?这恰好是标准音高中央A的频率
我们发现,每一个频率与音高对应的不能说大同小异,只能说非常完美。
其实Au带一个分析频率音高功能,但我认为上面这些分析能说明这一步骤的合理性
于是我们转成音高:
B2 A4
D3 E2
E3 D2
B3 F3
A2 B2
E4 C5
F2 C2
A4 B3
D2 E4
B4 A3
F3 D3
C4 F4
D4 C3最后一步,我们观察这些音高,发现什么?
没有sol
sol -> G
什么东西不包含G呢?十六进制
于是:
hz = [
(0xB2, 0xA4),
(0xD3, 0xE2),
(0xE3, 0xD2),
(0xB3, 0xF3),
(0xA2, 0xB2),
(0xE4, 0xC5),
(0xF2, 0xC2),
(0xA4, 0xB3),
(0xD2, 0xE4),
(0xB4, 0xA3),
(0xF3, 0xD3),
(0xC4, 0xF4),
(0xD4, 0xC3),
]注意到,两位十六进制数刚好表示0-255。
Part Ⅳ
现在我们有了256个高斯素数,有了13×2个不超过256的整数,需要找到13个10位整数。
接下来呢?
我们回到解密最开头的那句话:
故事,要从哥德巴赫猜想讲起。
哥德巴赫猜想:任何一个大于二的偶数都可以被表示为两个素数之和。
素数之和?我们发现:现在得到的所有素数都是大于9e9小于1e10的,这意味着,任两个素数的和刚好为10位数,与exe中要求相符合
如何从256个素数中挑选13×2个进行加和?下标
以Ⅲ中得到的数作为Ⅱ中素数的下标,并求和,我们得到了13个10位整数。
这就是答案
1996503118
1996507134
1996507030
1996506918
1996503082
1996506770
1996507710
1996503126
1996507050
1996503150
1996508182
1996507766
1996506018CORRECT!
Part V
"a 3-digit prime"
显然,3位质数只有143个显然枚举可过
好了还是按正常思路来,但我是枚举过的
仔细思考还有哪些没有被利用的信息
我们发现 puzzle.wav 中,我们只利用了其频率信息。
kaiyi: 我憋不住了
kaiyi: 一首音乐能有什么构成?
kaiyi: 有什么东西能是3位数
kaiyi: 在音乐中找数字你能想到什么
好的bpm
我们用 60 除以每一段持续时间(~0.472s)
$ 60 \div 0.472 \approx 127$
至此#0结束
the end