P2597 [ZJOI2012] 灾难

题目背景

阿米巴是小强的好朋友。

阿米巴和小强在草原上捉蚂蚱。小强突然想，如果蚂蚱被他们捉灭绝了，那么吃蚂蚱的小鸟就会饿死，而捕食小鸟的猛禽也会跟着灭绝，从而引发一系列的生态灾难。

学过生物的阿米巴告诉小强，草原是一个极其稳定的生态系统。如果蚂蚱灭绝了，小鸟照样可以吃别的虫子，所以一个物种的灭绝并不一定会引发重大的灾难。

题目描述

我们现在从专业一点的角度来看这个问题。我们用一种叫做食物网的有向图来描述生物之间的关系：

• 一个食物网有 $n$ 个点，代表 $n$ 种生物，生物从 $1$ 到 $n$ 编号。
• 如果生物 $x$ 可以吃生物 $y$，那么从 $y$ 向 $x$ 连一个有向边。
• 这个图没有环。
• 图中有一些点没有连出边，这些点代表的生物都是生产者，可以通过光合作用来生存。
• 而有连出边的点代表的都是消费者，它们必须通过吃其他生物来生存。
• 如果某个消费者的所有食物都灭绝了，它会跟着灭绝。

我们定义一个生物在食物网中的“灾难值”为，如果它突然灭绝，那么会跟着一起灭绝的生物的种数。

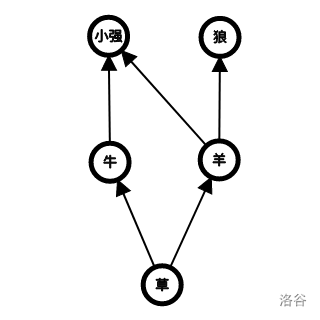
举个例子：在一个草场上，生物之间的关系如下

如果小强和阿米巴把草原上所有的羊都给吓死了，那么狼会因为没有食物而灭绝，而小强和阿米巴可以通过吃牛、牛可以通过吃草来生存下去。所以，羊的灾难值是 $1$。但是，如果草突然灭绝，那么整个草原上的 $5$ 种生物都无法幸免，所以，草的灾难值是 $4$。

给定一个食物网，你要求出每个生物的灾难值。

输入格式

第一行有一个整数，表示食物网的结点个数 $n$。

第 $2$ 到第 $(n + 1)$ 行，每行若干个互不相同的整数，第 $(i + 1)$ 行的整数 $a_{i, j}$ 表示编号为 $i$ 的生物可以吃编号为 $a_{i, j}$ 的生物。每行结尾有一个整数 $0$ 表示本行结束。

输出格式

输出 $n$ 行，每行一个整数，第 $i$ 行输出编号为 $i$ 的生物的灾难值。

样例 #1

样例输入 #1

5
0
1 0
1 0
2 3 0
2 0

样例输出 #1

4
1
0
0
0

提示

样例 1 解释

样例输入描述了题目描述中举的例子。

数据规模与约定

• 对于 $50\%$ 的数据，保证 $n \leq 10^4$。
• 对于 $100\%$ 的数据，保证 $1 \leq n \leq 65534$，$1 \leq a_{i, j} \leq n$，输入的文件大小不超过 1 MB，且图上不存在环。

题目简意

问一个DAG(有向无环图)上每个点可以支配多少个点

支配点

当从起点到达点 $v$ 的路径上必定存在点 $u$ ，那么称 $u$ 为 $v$ 的支配点， $u$ 支配 $v$。

支配树

根据支配点定义，容易发现，一个点的所有支配点一定在一条链上。

考虑反证法，如果存在某个点存在两个不在一条链上的支配点，那么这两个支配点都无法单独支配那个点，那么这两个点都不能成为那个点的支配点，矛盾，证毕。

那么每个点都会有且仅有一个最近的支配点，每个点都将这个点作为自己的父节点，就可以构建出来一片森林，这些树就称作这个DAG的支配树。我们可以把所有树的根连到一起，这样就只用操作一棵树了。

构建支配树

我们发现，如果我们构建出支配树，那么每个点的 $size-1$就是答案。

一个点的最近的支配点是哪个呢？

我们发现，如果我们已经把一个点所有入度的点全部构建到支配树中了，那么这些点在支配树上的lca（最临近公共祖先）就是它的支配点，那么他就被加入了支配树，注意找lca要用倍增优化。

这个操作需要保证 “我们已经把一个点所有入度的点全部构建到支配树中了” 。
你说的对，拓扑排序即可。

简单吧，代码如下：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 65536;
int n;
vector<int> G[N];//找儿子们
vector<int> F[N];//找爸爸们
vector<int> T[N];//支配树
int d[N][20];//倍增
int deg[N];//度数
int dep[N];//深度
int sz[N];//子树大小
queue<int> q;//拓排队列
int LCA(int u,int v){
    if(dep[u] < dep[v])swap(u,v);
    for(int i=19;i>=0;i--){
        if(dep[d[u][i]]>=dep[v])u=d[u][i];
    }
    if(u==v)return u;
    for(int i=19;i>=0;i--){
        if(d[u][i]!=d[v][i])u=d[u][i],v=d[v][i];
    }
    return d[u][0];
}
void tpo(){
    q.push(0);
    while(!q.empty()){
        int u = q.front();q.pop();
        for(auto v:G[u]){
            deg[v]--;
            if(!deg[v]){
                q.push(v);
                int lca = F[v][0];
                for(size_t i=1;i<F[v].size();i++){//求lca
                    lca = LCA(lca,F[v][i]);
                }
                d[v][0] = lca;
                T[lca].push_back(v);
                for(int i=1;i<20;i++)d[v][i] = d[d[v][i-1]][i-1];
                dep[v] = dep[lca] + 1;
            }
        }
    }
}
void dfs(int u){
    sz[u] = 1;
    for(auto v:T[u]){
        dfs(v);
        sz[u] += sz[v];
    }
    return ;
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    cin>>n;
    for(int i=1,t;i<=n;i++){
        cin>>t;
        for(;t;cin>>t)G[t].push_back(i),F[i].push_back(t),deg[i]++;
    }
    for(int i=1;i<=n;i++){
        if(deg[i]==0)G[0].push_back(i),F[i].push_back(0),deg[i]++;
    }
    tpo();
    dfs(0);
    for(int i=1;i<=n;i++)cout<<sz[i]-1<<'\n';
    return 0;
}