考虑到理解,代码阅读与打字交流的便利,先将术语名称统一如下:
NN:神经网络
hyper_parameters:超参数
learning_rate:学习率(数学公式表达: $\alpha$ )
epoch / epochs:更新轮数
batch:一个训练样本集
batch_size:一个训练样本集的样本数
parameters:参数
weight / weights:权重 (数学公式表达: $W$ ,表示一个矩阵)
bias:偏置 (数学公式表达: $B$ ,表示一个矩阵)
layer:层 (数学公式表达: $L$ ,表示一个序号)
input_layer:输入层 (数学公式表达: $x$ ,表示一个向量)
hidden_layer:隐藏层 (数学公式表达: $h$ ,表示一个向量)
output_layer:输出层 (数学公式表达: $o$ ,表示一个向量)
label / target:目标值(数学公式表达: $y$ ,表示一个向量)
另:也有记输出为 $y$ ,目标值为 $y^*$ ,$\hat{y}$
上角标(superscript):
$W^{[L]}$ 表示第 $L$ 层的参数。
【RNN】$W^{(t)}$ 表示第 $t$ 时刻的参数。
下角标(subscript):
$W^{[L]}_{i}$ 表示第 $L$ 层的第 $i$ 个参数。
forward:前馈
back propagation(BP):反向传播,backward
loss:损失函数(数学公式表达: $L$ ,表示一个函数/层)
定义为一个NN对样本集中的全体样本的偏差程度
MAE(Mean Absolute Error:平均绝对误差)
MSE(Mean Square Error:均方误差)
RMSE(Root Mean Square Error:均方根误差)
Cross-entropy(交叉熵损失函数) 交叉熵是用来评估当前训练得到的概率分布与真实分布的差异情况。 它刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近。
Activation Function:激活函数
sigmoid:$\frac{1}{e^{-x}+1}$,值域为$(0,1)$(数学公式表达: $\sigma$ ,表示一个函数)
(有时直接借 $\sigma$ 代表激活函数)
ReLU:线性整流函数(Linear rectification function),又称修正线性单元$ReLU(x)=max(0,x)$(数学公式表达: $ReLU$ ,表示一个函数)
softmax:归一化指数函数:
$$ o_i=Softmax(h^{[L]}_{i})=\frac{\exp({h^{[L]}_{i}})}{\sum_{j}\exp({h^{[L]}_{j}})} $$
log_softmax:$\ln(Softmax(x))$
前馈公式:
$$ h^{[L]} = \sigma(W^{[L]}h^{[L-1]}+B^{[L]}) $$
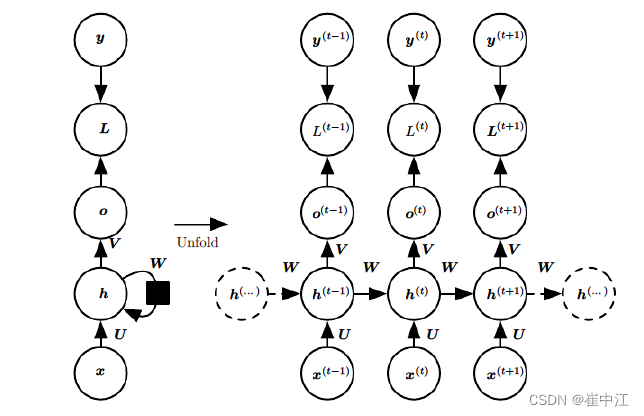
RNN:
- $x(t)$ 代表在序列索引 $t$ 时训练样本的输入,同样的, $x^{(t-1)}$ 和 $x^{(t+1)}$ 代表在序列索引号 $t-1$ 和 $t+1$ 时训练样本的输入。
- $h^{(t)}$ 代表在序列索引号 $t$ 时模型的隐藏状态, $h^{(t)}$ 由 $x^{(t)}$ 和 $h^{(t-1)}$ 共同决定。
- $o^{(t)}$ 代表在序列索引号 $t$ 时模型的输出, $o^{(t)}$ 只由模型当前的隐藏状态 $h^{(t)}$ 决定。
- $L^{(t)}$ 代表在序列索引号 $t$ 时模型的损失函数。
- $y^{(t)}$ 代表在序列索引号 $t$ 时训练样本序列的真实输出。
- $U,W,V$ 这三个矩阵是我们模型的参数,它在整个RNN模型中是共享的,这点和DNN不相同。也正是因为共享,体现了RNN模型的“循环反馈”思想。