堆是好东西啊！

你看，代码可短可短了：

#include<iostream>
#include<cstdlib>
#include<vector>
using namespace std;
template <typename Val>
class heap{
    public:
        heap(){size_h=0;}
        void push(Val x){size_h++;while(v.size()<=size_h)v.push_back(0);v[size_h]=x;up(size_h);}
        void pop(){_swap(v[1],v[size_h]),size_h--,down(1);}
        Val top(){return v[1];} 
        int size(){return size_h;}
        void print(){for(auto i:v)cout<<i<<' ';cout<<endl;}
    private:
        vector<Val>v;int size_h;
        void _swap(Val &a,Val &b){Val tmp=a;a=b;b=tmp;}
        void up(int x){if(x==1)return;if(v[x>>1]<v[x])_swap(v[x>>1],v[x]),up(x>>1);}
        void down(int x){
            int son=x<<1;
            if(son>size_h)return;else if(son<size_h && v[son]<v[son+1])son++;
            if(v[x]<v[son])_swap(v[son],v[x]),down(son);
            return;
        }
};
struct node{
    int val;
    node(){}
    node(int x){val=x;}
    bool operator<(const node &x)const{
        return val>x.val;
    }
};
heap<node>a;
int n;
int main(){
    srand(time(0));
    cin>>n;
    int t;
    for(int i=0;i<n;i++)cin>>t,a.push(node(t));
    for(int i=0;i<n;i++,a.pop())cout<<a.top().val<<' ';
    return 0;
}

我保证没压行（（（（（（（（

更重要的是，它比快排好写多了啊啊啊啊啊啊！！！

好吧我承认它其实本来长这样：

#include <iostream>
#include <cstdlib>
#include <vector>
using namespace std;
template <typename Val>
class heap
{
public:
    heap() { size_h = 0; }
    void push(Val x)
    {
        size_h++;
        while (v.size() <= size_h)
            v.push_back(0);
        v[size_h] = x;
        up(size_h);
    }
    void pop() { _swap(v[1], v[size_h]), size_h--, down(1); }
    Val top() { return v[1]; }
    int size() { return size_h; }
    void print()
    {
        for (auto i : v)
            cout << i << ' ';
        cout << endl;
    }

private:
    vector<Val> v;
    int size_h;
    void _swap(Val &a, Val &b)
    {
        Val tmp = a;
        a = b;
        b = tmp;
    }
    void up(int x)
    {
        if (x == 1)
            return;
        if (v[x >> 1] < v[x])
            _swap(v[x >> 1], v[x]), up(x >> 1);
    }
    void down(int x)
    {
        int son = x << 1;
        if (son > size_h)
            return;
        else if (son < size_h && v[son] < v[son + 1])
            son++;
        if (v[x] < v[son])
            _swap(v[son], v[x]), down(son);
        return;
    }
};
struct node
{
    int val;
    node() {}
    node(int x) { val = x; }
    bool operator<(const node &x) const
    {
        return val > x.val;
    }
};
heap<node> a;
int n;
int main()
{
    srand(time(0));
    cin >> n;
    int t;
    for (int i = 0; i < n; i++)
        cin >> t, a.push(node(t));
    for (int i = 0; i < n; i++, a.pop())
        cout << a.top().val << ' ';
    return 0;
}

但其实，这才是最开始的代码：

#include<iostream>
#include<cstdlib>
#include<vector>
using namespace std;
template <typename Val>
class heap{
    public:
        heap(){size_h=0;}
        void push(Val x){
            size_h++;
            while(v.size()<=size_h)v.push_back(0);
            v[size_h]=x;
            up(size_h);
        }
        void pop(){
            _swap(v[1],v[size_h]);
            size_h--;
            down(1);
        }
        Val top(){
            return v[1];
        } 
        int size(){
            return size_h;
        }
        void print(){
            for(auto i:v)cout<<i<<' ';
            cout<<endl;
        }
    private:
        vector<Val>v;
        int size_h;
        void _swap(Val &a,Val &b){
            Val tmp=a;
            a=b;
            b=tmp;
        }
        int ls(int x){
            return x<<1;
        }
        int rs(int x){
            return (x<<1)+1;            
        }
        int fa(int x){
            return x>>1;
        }
        void up(int x){
            if(x==1)return;
            if(v[fa(x)]<v[x]){
                _swap(v[fa(x)],v[x]);
                up(fa(x));
            }
            return;
        }
        void down(int x){
            if(ls(x)>size_h)return;
            if(rs(x)>size_h){
                if(v[x]<v[ls(x)]){
                    _swap(v[ls(x)],v[x]);
                    down(ls(x));
                }
            }
            else {
                if(v[ls(x)]<v[rs(x)]){
                    if(v[x]<v[rs(x)]){
                        _swap(v[rs(x)],v[x]);                    
                        down(rs(x));
                    }
                }
                else{
                    if(v[x]<v[ls(x)]){
                        _swap(v[ls(x)],v[x]);
                        down(ls(x));
                    }
                }
            }
            return;
        }
};
struct node{
    int val;
    node(){}
    node(int x){val=x;}
    bool operator<(const node &x)const{
        return val>x.val;
    }
};

int n;
heap<node>a;
int main(){
    srand(time(0));
    cin>>n;
    int t;
    for(int i=0;i<n;i++){
        cin>>t;
        a.push(node(t)); 
    }
    for(int i=0;i<n;i++){
        cout<<a.top().val<<' ';
        a.pop();
    }
    return 0;
}

堆听起来码量很大，其实你看压完行了并不多。

以上代码，只需要一个STD:priority_queue

手打显然方便理解。

解决问题：如何动态维护一个集合的最大值，包括插入任意元素与查询并删除最大元素？

我们考虑朴素的$O(n^2)$做法：插入排序。

因为有删除操作，如果只维护最大值，删除操作就是$O(n)$的；

因为有插入操作，如果维护完整排序，插入操作就是$O(n)$的。

有人会不会想到用二分去快速查找相应位置？

很可惜，二分不能支持链表操作。插入排序的swap方法依然会将复杂度退化到$O(n)$。

这叫做复杂度不平衡，如果一种操作过多就会导致复杂度爆炸。

当我们将两个操作都改为$O(\log n)$的，这个操作就叫复杂度均摊。（这也是OI的常用技巧）

考虑这样一件事，每次我删去最大值后，取而代之的就是次最大值，有没有办法去很快的维护这个次最大值呢？

我们要是每次以第一个插入的数为标准，把接下来要插入的数划分成比它大的和比他小的，这样我每次找次大值的时候只用在更大的一部分去找就好了。

我要是将数划成k部分，这样插入的复杂度为$O(k)$，那么每次查找次大值的时候就是$O(\frac nk)$的复杂度，为了复杂度均摊，我们一般取$k=\sqrt n$，这样，总复杂度就从$O(n^2)$降为$O(n\sqrt n)$。

这个思想，叫做分块。

但显然这不是我们今天的主题。

我们想这样一个操作：

我们如果维护每个数对于的它的次大值，这样当它作为最大值的时候，不用找就能知道它的次大值，方便了删除操作。

但是显然，这将拉出一条长长的链表，我们插入操作变得很麻烦。

但这是在每个数只有一个独生子的情况下。

那我们现在开放二胎，这次不严格要求儿子是所有数中最次大的，只要不超过自己就好。

我们对于每个数，维护其长子和次子，当父亲因公离任或殉职，就挑出长子继任。

当皇帝驾崩（整个集合中的最大值被删除）时，就直接挑出其太子继位，而太子就挑他的长子来取代自己原来的位置。

依次类推，直到重孙子没有儿子。

这就完成了一次删除操作。

那这次删除操作的复杂度是多少呢？

没儿子的N重孙子是皇帝的第几世孙，我们就要继任多少次，也就是复杂度。

我们皇帝有2个儿子

这两个儿子也有各有两个儿子，皇帝有4个孙子

1,2,4,8,16,……依次类推。

当我们数到第二世时，有$1+2=3=2^2-1$个皇族亲世；

第三世，则是$1+2+4=7=2^3-1$个。

也就是说，当有$n$世皇室的时候，我们就可以处理$2^n$级别的皇亲皇子了。

换句话说，当我们有$n$个儿子在族谱里时，最多只有$log_2n$世皇室。

这样，我们皇帝驾崩一次的复杂度就是$O(logn)$的复杂度了。

那，有外戚要入族（插入元素）呢？

既然是外戚，就得一层层升级来看自己的辈分。

先找一个辈分最高但儿子不足两个的皇室认个义父，找辈分高的能让辈分最低的皇室辈分尽量高，这样保证要连续继位的复杂度不会退化。

然后，毕竟是外戚要来专权，本身还是有些实力的，所以当实力足够（自己的值比其父亲大）时，会把其父亲踹下来，自己提高一个辈分，而本来的父亲当自己的儿子。显然，另一个儿子依然可以乖乖当自己儿子。

就这样一层层的打怪父升级，要是实力不够就不打了乖乖当儿子，否则直到把皇帝弄成太子才会停下来。

这样，易证，外戚实力入侵一次也最多把自己的所有长辈全部干掉就好了，复杂度$O(logn)$。

于是，插入和删除操作都变成了$O(logn)$的复杂度了。

用算法语言表达上述内容即是：

删除操作：
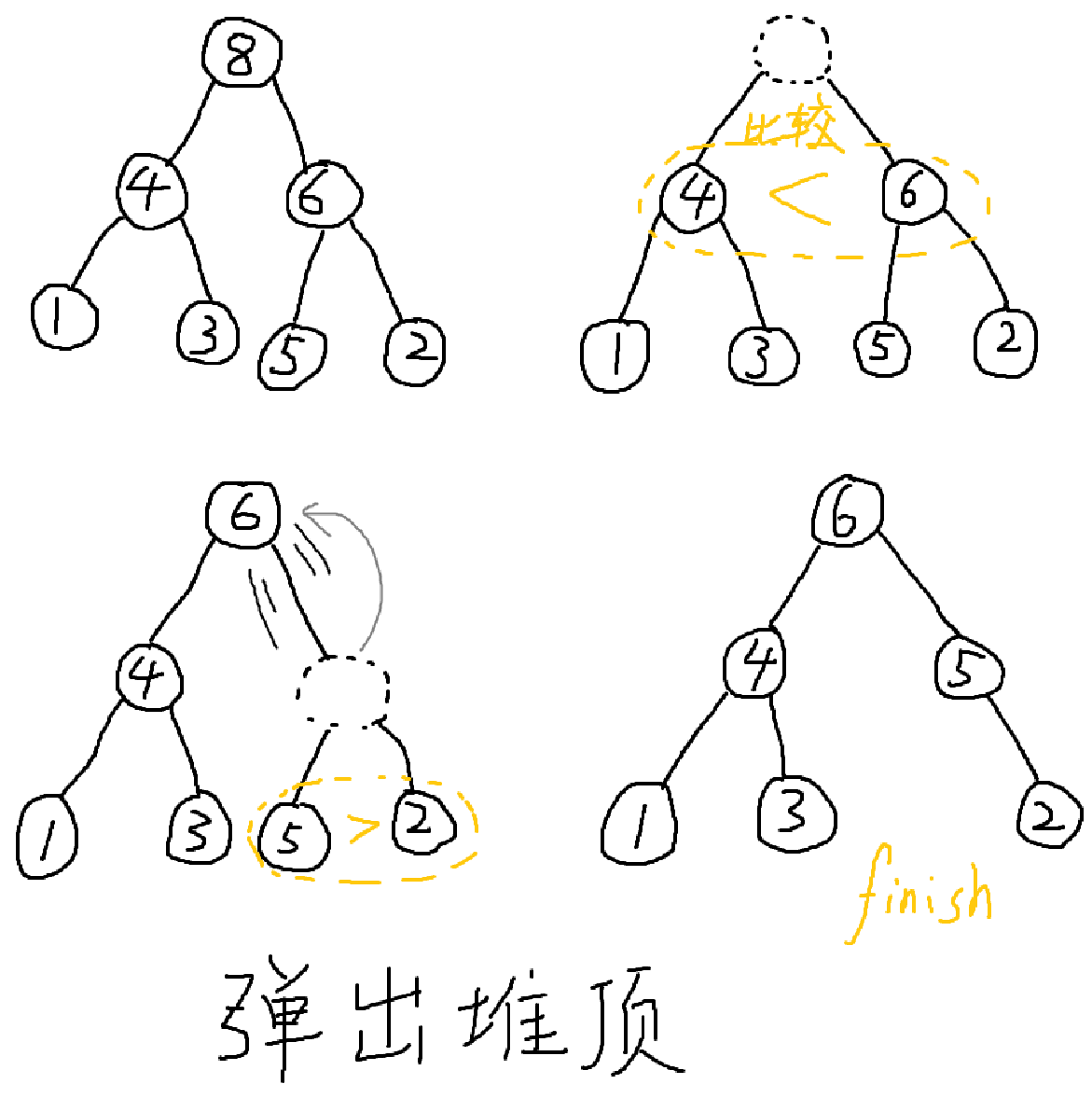
将树的根节点值清空，选择其左右儿子节点中值更大的节点赋值给它，在递归那个儿子，直到递归到叶子节点结束。
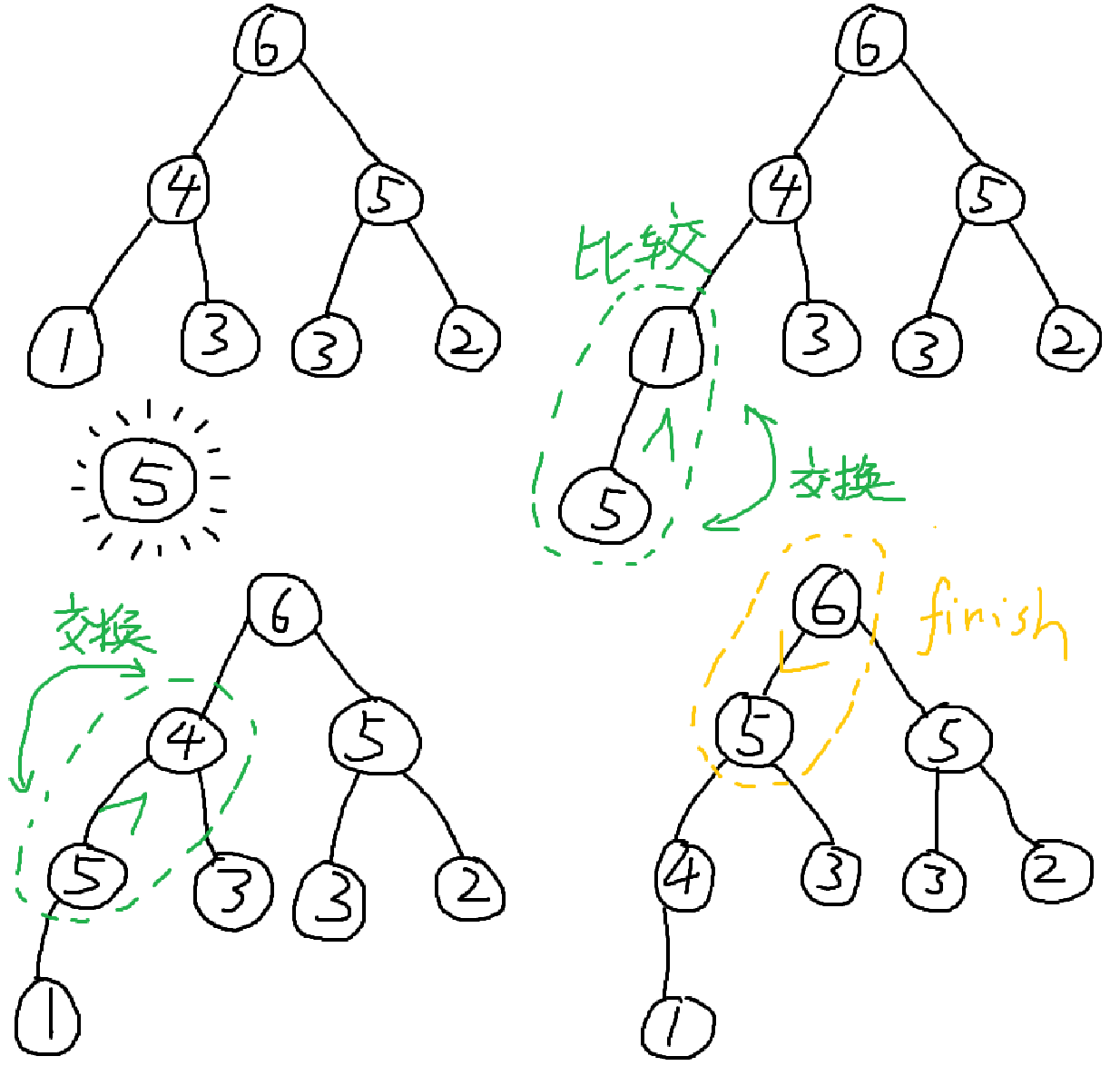
插入操作：
在这颗完全二叉树的末尾位置加一个元素，然后递归向上更新，不断与父节点比较，如果比父节点更大就交换两值。

这，就是二叉堆了。

当然，这个堆既然叫堆，有些名字就要改，比如树根就叫堆顶，删除树根元素就叫弹出堆顶元素，等等。

写成代码一点不难，比快排的细节少多了。

由于是一个二叉树，我们就用写线段树用的技巧：广搜顺序编号，根节点编号为1,找规律不难发现一个数的左儿子的自己编号的两倍，右儿子编号是左儿子编号加一。

这样我们就能迅速的写出一个堆了。

#include<iostream>
#include<cstdlib>
#include<vector>
using namespace std;
template <typename Val>
class heap{
    public:
        heap(){size_h=0;}//初始化堆的大小为0
        void push(Val x){size_h++;while(v.size()<=size_h)v.push_back(0);v[size_h]=x;up(size_h);}//插入元素
        void pop(){_swap(v[1],v[size_h]),size_h--,down(1);}//弹出堆顶
        Val top(){return v[1];}//返回堆顶元素值 
        int size(){return size_h;}//返回堆的大小
        void print(){for(auto i:v)cout<<i<<' ';cout<<endl;}//调试用的
    private:
        vector<Val>v;int size_h;//堆的本体
        void _swap(Val &a,Val &b){Val tmp=a;a=b;b=tmp;}//定义一个swap（其实不用）
        void up(int x){if(x==1)return;if(v[x>>1]<v[x])_swap(v[x>>1],v[x]),up(x>>1);}//向上更新
        void down(int x){//向下更新
            int son=x<<1;
            if(son>size_h)return;else if(son<size_h && v[son]<v[son+1])son++;
            if(v[x]<v[son])_swap(v[son],v[x]),down(son);
            return;
        }
};
struct node{
    int val;
    node(){}
    node(int x){val=x;}
    bool operator<(const node &x)const{
        return val>x.val;//重载运算符使得大根堆变小根堆
    }
};
heap<node>a;
int n;
int main(){
    srand(time(0));
    cin>>n;
    int t;
    for(int i=0;i<n;i++)cin>>t,a.push(node(t));//压入堆
    for(int i=0;i<n;i++,a.pop())cout<<a.top().val<<' ';//弹出堆
    return 0;
}