N0244. 小明去旅游【NOIP2023模拟赛T1】

题目描述

$3202$年$8$月$21$日，小明去西安旅游，发现地铁站已经有$n$个了。

地铁站编号成数字$1,2,...,n$。在特定的地铁站，你可以购买特定的地铁票，地铁票一共有$m$种。

每一张票可以由四个参数$i,l,r,w$表示：你可以从第$i$个地铁站，花费$w$元买一张票，然后从$i$出发坐地铁，在地铁站$[l,r]$之间的任意一站下车。

小明想知道，从地铁站$1$出发，最少要花多少钱才能到达其他地铁站，请帮小明算一下吧。

输入格式

第一行两个正整数$n,m$。

接下来$m$行，每行四个参数$i,l,r,w$。

输出格式

输出$n$个整数，表示答案，如果没法到达，输出$−1$。

样例输入1

3 2
1 2 2 10
2 1 3 1

样例输出1

0 10 11

样例输入2

3 3
1 2 2 10
2 1 3 1
1 1 3 15

样例输出2

0 10 11

数据范围

对于30%的数据：$1\leq n\leq 1000,1\leq m \leq 2000$。

对于70%的数据：$1\leq n \leq 10^5,1\leq m \leq 2\times 10^5$。

对于100%的数据：$1\leq n \leq 5\times 10^5，1\leq m \leq 10^6。1\leq i\leq n,1\leq l\leq r\leq n,1\leq w\leq 10^9$。

题解

考虑怎么样做单源最短路：

如果直接建图连边，还没跑最短路，空间复杂度$O(mn)$。

那么边是连不了的。

考虑朴素的dij为啥不行。

因为边太多队列炸了（。。。。

其实一把边不至于拆开往队列里加，从某个点伸出去的一大把边的dis都一样，优先级一样，直接存一个{dis,l,r}就好了。

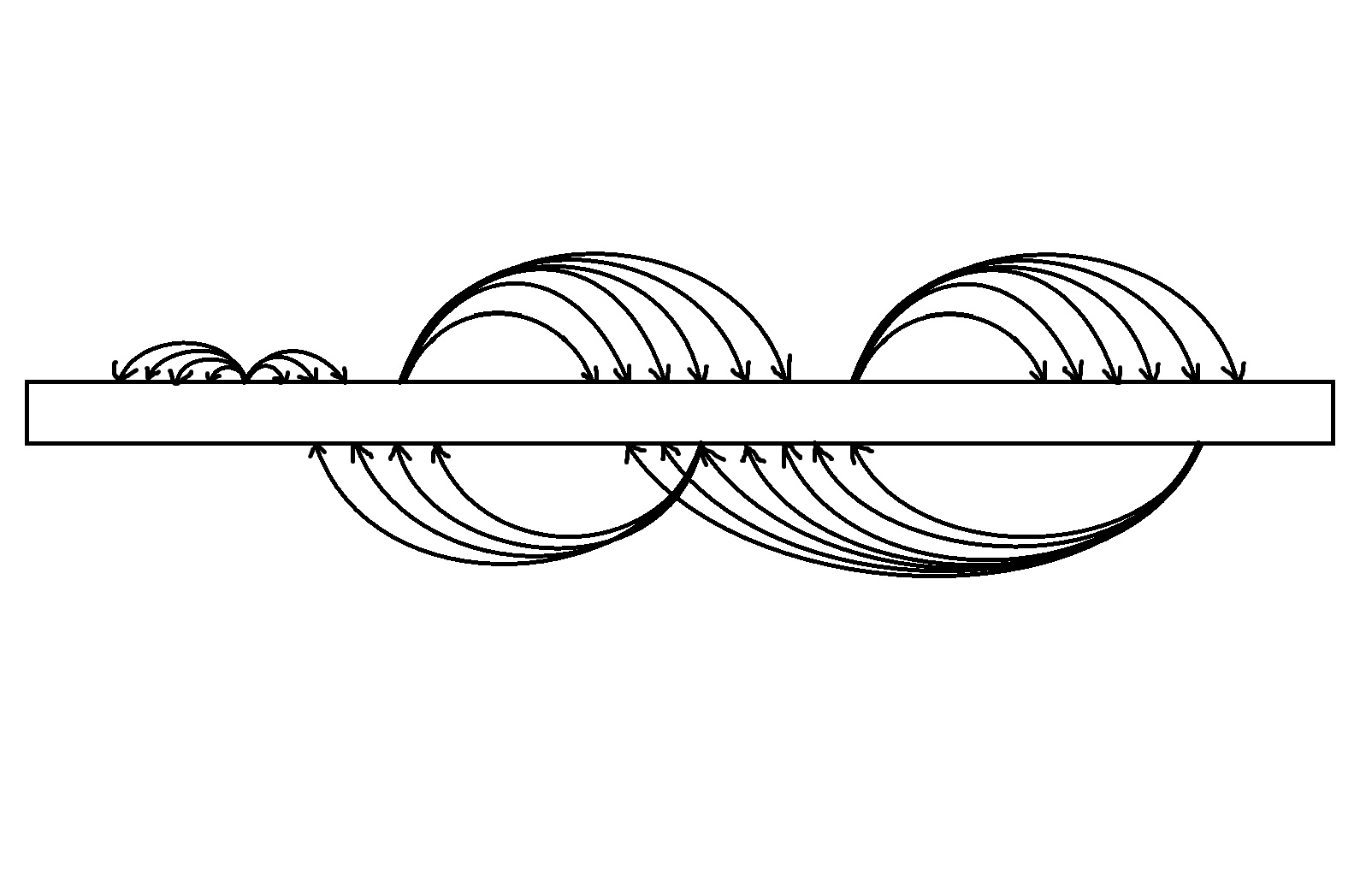
上个图：

pPGaWAx.jpg
pPGaWAx.jpg

就变回了：

pPGa2H1.jpg
pPGa2H1.jpg

那问题在哪？

问题在于访问了太多vis[i]==true的点，虽然continue;了答案不会错。

那怎么做到不访问vis[i]==true的点呢？

考虑校门外的树这道题：初始一个满区间，每次将一个区间的全部树砍掉，问还剩几棵树？

你发现了，这也是存在一棵树砍太多遍的问题。

如果你用线段树$O(nlogn)$当我没说，但这道题可以几乎线性做法。

那就是并查集。对于每个点，以它右边（包括自己）第一个没被访问过的点为祖先。

这样再遍历每个区间时就可以像遍历链表一样轻松了

代码：for(int i=l;i<=r;i=find(i))

说到链表，这不就是链表删数操作？

用数组下标模拟链表，就可以通过下标删数了。

这样子，因为vis[]只会被以某种方式遍历一遍，所以复杂度约是线性。

#include<cstdio>
#include<cstring>
#include<queue>
#include<bits/basic_string.h>
#define int long long 
using namespace std;
inline int read(){
    int s=0,f=1;char c=getchar();
    while(c<48 || c>57){if(c=='-')f=-f;c=getchar();}
    while(c>=48 && c<=57)s=s*10+c-48,c=getchar();
    return s*f;
}
int n,m;
const int MAXM=1e6+10; 
const int MAXN=5e5+10; 
struct node{
    int w,l,r;
    node(){}
    node(int a,int b,int c){w=a,l=b,r=c;}
    bool operator<(const node &x)const{
        return w>x.w;
    }
};
basic_string <node> edge[MAXM]; 
priority_queue<node> q;
int dis[MAXN];
int lst[MAXN],nxt[MAXN];
void init(){//初始化链表
    for(int i=1;i<=n;i++){
        lst[i]=i-1;
        nxt[i]=i+1;
    }
    return ;
}
bool vis[MAXN];
void del(int x){
    nxt[lst[x]]=nxt[x];
    lst[nxt[x]]=lst[x];
}
void bfs(){//最短路
    q.push(node(0,1,1));
    dis[1]=0;   
    while(!q.empty()){
        int w=q.top().w,l=q.top().l,r=q.top().r;
        q.pop();
        for(int i=l;i<=r;i=nxt[i]){
            if(vis[i])continue;//第一个还是得访问
            dis[i]=w;//这个点的最短路确定了
            for(auto it:edge[i]){
                q.push(node(w+it.w,it.l,it.r));
            }
            vis[i]=1;//。。。
            del(i);//删点
        }
    }
    return;
}
signed main(){
    int id,l,r,w;
    memset(dis,-1,sizeof(dis));
    n=read(),m=read();
    init();
    for(int i=0;i<m;i++){
        id=read();l=read();r=read();w=read();
        edge[id]+=node(w,l,r);
    }    
    bfs();
    for(int i=1;i<=n;i++){
        printf("%lld ",dis[i]);
    }
    return 0;
}