树上染色|P3177
https://www.luogu.com.cn/problem/P3177
首先:
%%%%%WVR CCCCCCCCCCCCCCCCCCCCCCCCCCCCCOrz
%%%%%WVR CCCCCCCCCCCCCCCCCCCCCCCCCCCOrz
%%%%%WVR CCCCCCCCCCCCCCCCCCCCCCOrz
%%%%%WVR CCCCCCCCCCCCCCCOrz
%%%%%WVR CCCCCCCCCCOrz
%%%%%WVR CCCCCOrz
快去膜他!!!
想了一天(一下午+一晚自习+一早上)不会
(准确来说先开始想了一堆玄学假做法)
WVR一眼秒掉后$15minAC$掉了
给我讲了后,代码思路清新简洁,通俗易懂,从里到外流露出一股清雅之气
与各路tj不同,这转移可谓一股清流
导致我想清楚后$50min$写完代码样例一边过,交上去一遍$AC$,完全没任何调试空间好不好
才怪你tmd明明炸了一次long long
(那确实怪我)
所以为啥我这么菜?
正题
简要题意:
给一棵有n个点的无根树,你可以将$k$个点染为黑色,$n-k$个点染成白色。
记总收益为 所有黑点两两之间距离和 加上 所有白点两两之间距离和
问最大收益
首先我陷入了树上背包
但发现不会做
不管怎么转移,都转移的有问题
(你怎么那么会说废话呢?)
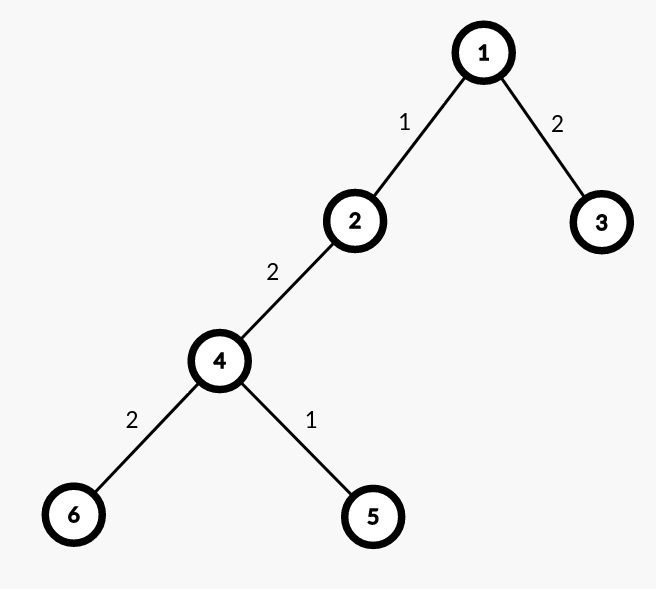
快see see这个图!
我遇到了什么问题呢?
我当时想把4的dp值求出来
于是访问其每个儿子
我当时就想,这个儿子的子树内有$n$个黑点,我要是此节点选黑,那么这条边就被贡献了$w \times k$,若选白,就是$w \times (sz[son]-k)$
但手动模拟时就发现了问题
如我现在要在4节点访问5
当总黑点数为$3$时,我用原来子树的黑点为$2$的$dp$值加上5节点子树黑点为$1$的$dp$值,再加上4,5这条边做的贡献,因为有此边左边$2$个黑点,右边$1$个黑点,所以被贡献了$2 \times 1$次
so 我算出来的dp值为$2 + 2 \times 2 \times 1 = 4$
但这不对啊,应该是$6$啊!
显然我6,4的边少贡献了一次
而且以后再也贡献不了了
什么?你说你没听懂!?!
你听懂了才说明你和我一样不正常呢
好了不需要懂上面的咱看vr给的做法
直接一段代码就无需多言了
//大抵是这样的
//我们现在已经合并了一部分(可以没有)子树
//现在要合并这个子树(儿子nxt的子树)
//其中,在原树中选x个黑点,要合并的的子树选y个黑点
//然后他就把我的问题解决了
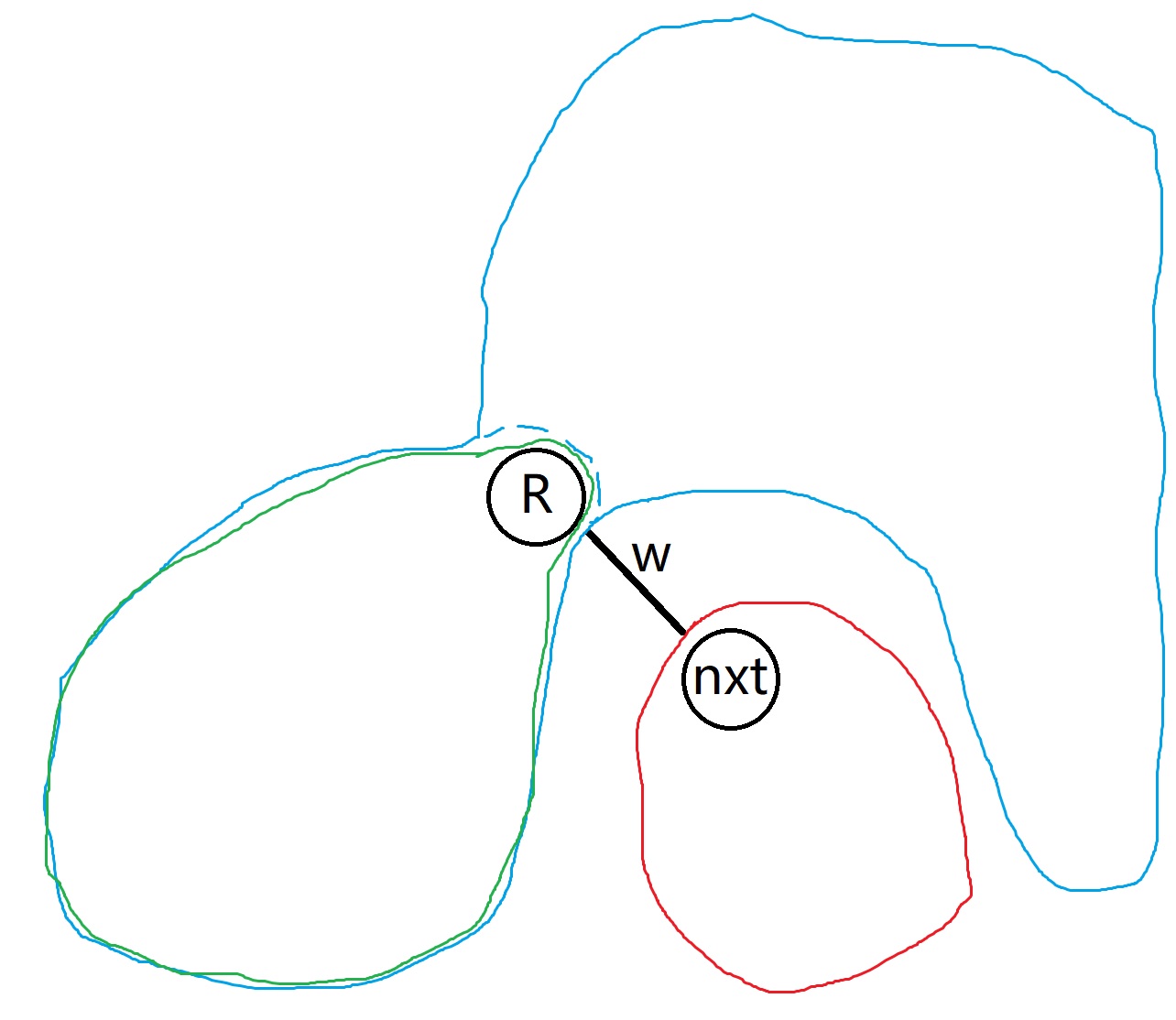
//啊我还是放一张图(要是vr手绘就好了)//绿圈表示已经合并好的集合(对贡献没啥用),红圈表示要合并的子树集
//蓝圈表示红圈的补集
//那么
//我们一旦确定了红圈内黑点的个数,这条边对全局的贡献就确定了!
inb=y,outb=m-inb;//红圈里的黑点inb,剩下的黑点都在蓝圈里
inw=sz[nxt]-y,outw=(n-m)-inw;//白点反之亦然。
val=edge[i].w*(inb*outb+inw*outw);//算一下此情此景的贡献
dp[r][x+y]=max(dp[r][x+y],dp[r][x]+dp[nxt][y]+val);//这个顺推转移够清楚吧!!!
//当然,x就转移这块有点用这几行核心代码让我幡然醒悟
尤其是
其根本没有调试空间!
去AC吧:
//vr讲了必须打出来
#include<iostream>
#include<cstring>
#define int long long
using namespace std;
int n,m;
const int MAXN=2e3+10;
struct tree{
int to;
int w;
int next;
}edge[MAXN*2];
int head[MAXN];
int _cnt=0;
void add(int u,int v,int w){
edge[++_cnt].to=v;
edge[_cnt].w=w;
edge[_cnt].next=head[u];
head[u]=_cnt;
}
int dp[MAXN][MAXN];
int sz[MAXN];
int tp[MAXN];
//vr讲的DP
void dfs(int r){
sz[r]=1;
dp[r][0]=0;//最少的价值是0罢了
dp[r][1]=0;//这是一个黑点的情况
int inb,outb,inw,outw;
for(int i=head[r];i!=0;i=edge[i].next){
int nxt=edge[i].to;
//一个一个子树合并
//与朴素的背包不同
//vr用更好理解的顺推写的
if(sz[nxt])continue;
dfs(nxt);
for(int x=0;x<=min(m,sz[r]);x++){//目前合并好的
for(int y=0;y<=min(m,sz[nxt]);y++){//要合并的
//对于这条边的贡献咋算捏
inb=y;
outb=m-inb;
inw=sz[nxt]-y;
outw=n-m-inw;
int val=edge[i].w*(inb*outb+inw*outw);
tp[x+y]=max(tp[x+y],dp[r][x]+dp[nxt][y]+val);
//vr教的小trick,如果不想仔细想dp转移滚动压维的细节,就开个临时数组防止覆盖
}
}
memcpy(dp[r],tp,sizeof(tp));//赋给它
memset(tp,-0x3f,sizeof(tp));//清空它
sz[r]+=sz[nxt];//这个更新sz罢了
}
return;//真就毫无细节
}
signed main(){
cin>>n>>m;
int u,v,w;
memset(dp,-0x3f,sizeof(dp));//这个细节vr是真滴严谨啊!题目没说w范围,他连负权边都考虑了 %%%wvr orz
for(int i=1;i<n;i++){
cin>>u>>v>>w;
add(u,v,w);
add(v,u,w);
}
dfs(1);
cout<<dp[1][m];
return 0;
}