括号树|P5658
https://www.luogu.com.cn/problem/P5658
题目背景
本题中合法括号串的定义如下:
()是合法括号串。- 如果
A是合法括号串,则(A)是合法括号串。 - 如果
A,B是合法括号串,则AB是合法括号串。
本题中子串与不同的子串的定义如下:
- 字符串
S的子串是S中连续的任意个字符组成的字符串。S的子串可用起始位置 l 与终止位置 r 来表示,记为 S(l,r)S(1≤l≤r≤∣S∣,∣S∣表示 S 的长度)。 S的两个子串视作不同当且仅当它们在S中的位置不同,即 l 不同或 r 不同。
题目描述
一个大小为 n 的树包含 n 个结点和 n-1 条边,每条边连接两个结点,且任意两个结点间有且仅有一条简单路径互相可达。
小 Q 是一个充满好奇心的小朋友,有一天他在上学的路上碰见了一个大小为 n 的树,树上结点从 1 ∼ n 编号,1 号结点为树的根。除 1 号结点外,每个结点有一个父亲结点,u(2≤u≤n)号结点的父亲为 fu(1≤fu\<u)号结点。
小 Q 发现这个树的每个结点上恰有一个括号,可能是( 或)。小 Q 定义 si 为:将根结点到 i 号结点的简单路径上的括号,按结点经过顺序依次排列组成的字符串。
显然 si 是个括号串,但不一定是合法括号串,因此现在小 Q 想对所有的 i(1≤i≤n)求出,si 中有多少个互不相同的子串是合法括号串。
这个问题难倒了小 Q,他只好向你求助。设 si 共有 ki 个不同子串是合法括号串, 你只需要告诉小 Q 所有 i×ki 的异或和,即:
(1×k1) xor (2×k2) xor (3×k3) xor ⋯ xor (n×kn)
其中 xor 是位异或运算。
输入格式
第一行一个整数 n,表示树的大小。
第二行一个长为 n 的由( 与) 组成的括号串,第 iii 个括号表示 iii 号结点上的括号。
第三行包含 n-1 个整数,第 i(1≤i\<n)个整数表示 i+1 号结点的父亲编号 fi+1。
输出格式
仅一行一个整数表示答案。
输入输出样例
输入 #1
5
(()()
1 1 2 2输出 #1
6说明/提示
【样例解释1】
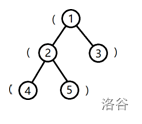
树的形态如下图:
将根到 1 号结点的简单路径上的括号,按经过顺序排列所组成的字符串为 (,子串是合法括号串的个数为 0。
将根到 2 号结点的字符串为 ((,子串是合法括号串的个数为 0。
将根到 3 号结点的字符串为 (),子串是合法括号串的个数为 1。
将根到 4 号结点的字符串为 (((,子串是合法括号串的个数为 0。
将根到 5 号结点的字符串为 ((),子串是合法括号串的个数为 1。
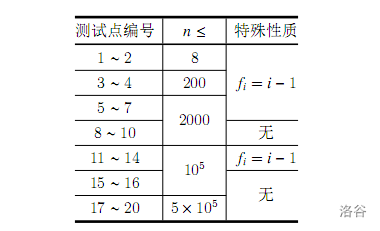
【数据范围】
这树很大,怕你把持不住,就用O(n)了。
那说明我们必须得通过父节点的答案推出子节点的答案
我们要找到一个能转移的DP
OK,现在有一个括号串,我们要维护哪些信息使得我们在其后加一个括号后能推出新的答案?
也就是说,我们看新加一个括号后会对答案怎样做出贡献。
如果是一个左括号,那确实对答案没啥贡献。
若是右括号, 将有两种贡献:
(****) 匹配左边最后一个未匹配的左括号,对答案贡献1
()()(**)(****) 新括号块与之前连续的括号块构成新子串,若之前有g个连续的括号块,则对答案贡献g
那我们维护这两个值及dp值就好了
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<vector>
#define int long long
using namespace std;
//记上一个未匹配的左括号
//记长度
int n;
const int MAXN=5e5+10;
inline int read(){//没卵用
int s=0,f=1;
char c=getchar();
while(c<48 ||c>57){if(c=='-')f=-f;c=getchar();}
while(c>=48 && c<=57)s=s*10+c-48,c=getchar();
return s*f;
}
string bracket;
int g[MAXN];//以i点结束的括号块的个数
int fa[MAXN];
int lst[MAXN];
int dp[MAXN];
vector <int> v[MAXN];
//硬头皮dp qmr说,这是一种新型DP
int ans=0;
void dfs(int x){
//当前节点往上看
if(bracket[x]=='('){
dp[x]=dp[fa[x]];
lst[x]=x;//维护上一个左括号
}
else{
// == ')'
//与上一个'('匹配
if(lst[fa[x]]>0){//如果还有上一个左括号
g[x]=g[fa[lst[fa[x]]]]+1;
dp[x]=dp[fa[x]]+g[x];//加贡献
lst[x]=lst[fa[lst[fa[x]]]];//拉法拉法~
}
else dp[x]=dp[fa[x]];
}
ans^=x*dp[x];//记答案
for(auto i:v[x]){
dfs(i);
}
}
signed main(){
n=read();
cin>>bracket;
bracket='!'+bracket;//移位
for(int i=2;i<=n;i++){
fa[i]=read();
v[fa[i]].push_back(i);
}
dfs(1);
cout<<ans;
return 0;
}