三色二叉树|P2585
https://www.luogu.com.cn/problem/P2585
题目描述
一棵二叉树可以按照如下规则表示成一个由 0、1、2 组成的字符序列,我们称之为“二叉树序列 S”:
S={0表示该树没有子节点1S1表示该树有一个节点,S1为其子树的二叉树序列2S1S2表示该树由两个子节点,S1和S2分别表示其两个子树的二叉树序列S= \begin{cases} 0\& \text表示该树没有子节点\\ 1S\_1\& 表示该树有一个节点,S\_1 为其子树的二叉树序列\\ 2S\_1S\_2\& 表示该树由两个子节点,S\_1 和 S\_2 分别表示其两个子树的二叉树序列 \end{cases}S=⎩⎪⎪⎨⎪⎪⎧01S12S1S2表示该树没有子节点表示该树有一个节点,S1为其子树的二叉树序列表示该树由两个子节点,S1和S2分别表示其两个子树的二叉树序列
(TMD LaTeX炸成这样您就不知道高抬贵手点一下我千辛万苦花费5秒钟点击四下鼠标触摸键盘三次小指持续唱跳rap篮球向计算机的键盘监听输入系统发送按键“^c^v”才粘贴来的link吗????????)
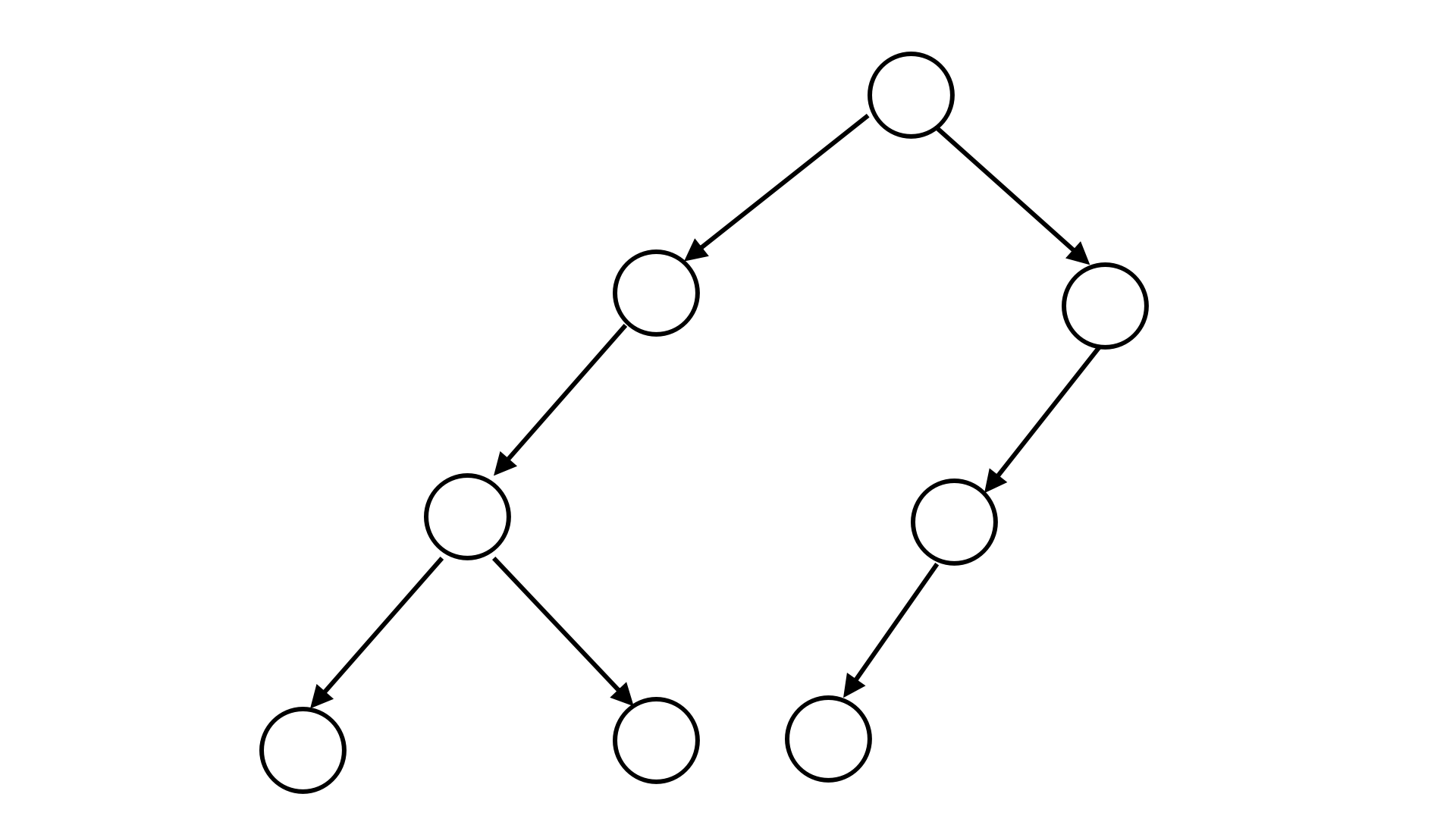
例如,下图所表示的二叉树可以用二叉树序列 S=21200110 来表示。
你的任务是要对一棵二叉树的节点进行染色。每个节点可以被染成红色、绿色或蓝色。并且,一个节点与其子节点的颜色必须不同,如果该节点有两个子节点,那么这两个子节点的颜色也必须不同。给定一颗二叉树的二叉树序列,请求出这棵树中最多和最少有多少个点能够被染成绿色。
输入格式
输入只有一行一个字符串 s,表示二叉树序列。
输出格式
输出只有一行,包含两个数,依次表示最多和最少有多少个点能够被染成绿色。
输入输出样例
输入 #1
1122002010输出 #1
5 2说明/提示
数据规模与约定
对于全部的测试点,保证 1≤∣s∣≤5×100000,s 中只含字符 0 1 2。
那,我们开始吧。
嗯。
思路
工欲善其事,必先利其器
题目给出了二叉树子节点个数的前序遍历,但,这并不方便我们dfs
那?
我们需要根据这个前序遍历建一棵树,方便我们dfs.
如果遍历到'0',那就可以return了;
如果遍历到'1',那它的下一个就是它的儿子;
如果遍历到'2',第一个儿子不变,第二个儿子是它第一个儿子子树上最靠后节点的下一个
于是一个正确的build就写出来了:
void build(int x){
cnt=max(cnt,x);
while(s[x]>'0'){
s[x]--;
v[x].push_back(cnt+1);//建树
build(cnt+1);
}
return;
}嗯——
那,
然后呢?
逐个击破
分类讨论DP就好啦
与精神分裂般的分支结构不同,DP的分类讨论总是“_蒙络摇缀,参差披拂_”的,互相影响,密不可分的。
这道题的DP比较好写,根据题意模拟即可
嗯?
我们可以设计状态dp[min/max][node][g/r/b],表示当前考虑了节点node及其子树,当前颜色选择红/绿/蓝时的最小值/最大值。
怎么转移呢?
当只有该节点只有一个儿子时,取儿子另外两个颜色的max/min就好了
有两个儿子时,注意,两个儿子的颜色不能相同,所以取剩下两种颜色不同对应方式的max/min
是绿色就要加一呀
dp[1][x][0]=max(dp[1][i][1],dp[1][i][2])+1;
dp[1][x][1]=max(dp[1][i][0],dp[1][i][2]);
dp[1][x][2]=max(dp[1][i][0],dp[1][i][1]);
dp[0][x][0]=min(dp[0][i][1],dp[0][i][2])+1;
dp[0][x][1]=min(dp[0][i][0],dp[0][i][2]);
dp[0][x][2]=min(dp[0][i][0],dp[0][i][1]);
dp[1][x][0]=max(dp[1][i][1]+dp[1][j][2],dp[1][i][2]+dp[1][j][1])+1;
dp[1][x][1]=max(dp[1][i][0]+dp[1][j][2],dp[1][i][2]+dp[1][j][0]);
dp[1][x][2]=max(dp[1][i][0]+dp[1][j][1],dp[1][i][1]+dp[1][j][0]);
dp[0][x][0]=min(dp[0][i][1]+dp[0][j][2],dp[0][i][2]+dp[0][j][1])+1;
dp[0][x][1]=min(dp[0][i][0]+dp[0][j][2],dp[0][i][2]+dp[0][j][0]);
dp[0][x][2]=min(dp[0][i][0]+dp[0][j][1],dp[0][i][1]+dp[0][j][0]);嗯——
哦对了,还要注意边界条件,如果递归到了叶子节点,它绿色的dp值一定是1,因为都选了绿色嘛
那就放代码喽
嗯~
#include<iostream>
#include<cstring>
#include<string>
#include<vector>
using namespace std;
string s;
const int MAXN=5e5+10;
vector <int> v[MAXN];
int cnt=0;
void build(int x){
cnt=max(cnt,x);
while(s[x]!=48){
s[x]--;
v[x].push_back(cnt+1);
build(cnt+1);
}
return;
}
int dp[2][MAXN][3];//1max0min 绿 红 蓝
void dfs(int x){
if(v[x].size()==1){
int i=v[x][0];
dfs(i);
dp[1][x][0]=max(dp[1][i][1],dp[1][i][2])+1;
dp[1][x][1]=max(dp[1][i][0],dp[1][i][2]);
dp[1][x][2]=max(dp[1][i][0],dp[1][i][1]);
dp[0][x][0]=min(dp[0][i][1],dp[0][i][2])+1;
dp[0][x][1]=min(dp[0][i][0],dp[0][i][2]);
dp[0][x][2]=min(dp[0][i][0],dp[0][i][1]);
}
else if(v[x].size()==2){
int i=v[x][0];
int j=v[x][1];
dfs(i);
dfs(j);
dp[1][x][0]=max(dp[1][i][1]+dp[1][j][2],dp[1][i][2]+dp[1][j][1])+1;
dp[1][x][1]=max(dp[1][i][0]+dp[1][j][2],dp[1][i][2]+dp[1][j][0]);
dp[1][x][2]=max(dp[1][i][0]+dp[1][j][1],dp[1][i][1]+dp[1][j][0]);
dp[0][x][0]=min(dp[0][i][1]+dp[0][j][2],dp[0][i][2]+dp[0][j][1])+1;
dp[0][x][1]=min(dp[0][i][0]+dp[0][j][2],dp[0][i][2]+dp[0][j][0]);
dp[0][x][2]=min(dp[0][i][0]+dp[0][j][1],dp[0][i][1]+dp[0][j][0]);
}
dp[1][x][0]=max(dp[1][x][0],1);
dp[0][x][0]=max(dp[0][x][0],1);
return;
}
signed main(){
cin>>s;
build(0);
dfs(0);
cout<<dp[1][0][0]<<' '<<min(dp[0][0][0],min(dp[0][0][1],dp[0][0][2]));
return 0;
}