运输计划|P2680

https://www.luogu.com.cn/problem/P2680

题目背景

公元 2044 年，人类进入了宇宙纪元。

题目描述

公元 2044 年，人类进入了宇宙纪元。

L 国有 n 个星球，还有 n-1 条双向航道，每条航道建立在两个星球之间，这 n-1条航道连通了 L 国的所有星球。

小 P 掌管一家物流公司， 该公司有很多个运输计划，每个运输计划形如：有一艘物流飞船需要从 ui 号星球沿最快的宇航路径飞行到 vi​ 号星球去。显然，飞船驶过一条航道是需要时间的，对于航道 j，任意飞船驶过它所花费的时间为 tj，并且任意两艘飞船之间不会产生任何干扰。

为了鼓励科技创新， L 国国王同意小 P 的物流公司参与 L 国的航道建设，即允许小 P 把某一条航道改造成虫洞，飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小 P 的物流公司就预接了 m 个运输计划。在虫洞建设完成后，这 m 个运输计划会同时开始，所有飞船一起出发。当这 m 个运输计划都完成时，小 P 的物流公司的阶段性工作就完成了。

如果小 P 可以自由选择将哪一条航道改造成虫洞， 试求出小 P 的物流公司完成阶段性工作所需要的最短时间是多少？

输入格式

第一行包括两个正整数 n,m，表示 L 国中星球的数量及小 P 公司预接的运输计划的数量，星球从 1 到 n 编号。

接下来 n-1 行描述航道的建设情况，其中第 i 行包含三个整数 ai,bi 和 ti，表示第 i 条双向航道修建在 ai 与 bi​ 两个星球之间，任意飞船驶过它所花费的时间为 ti。

数据保证

接下来 m 行描述运输计划的情况，其中第 j 行包含两个正整数 uj​ 和 vj，表示第 j 个运输计划是从 uj 号星球飞往 vj​号星球。

输出格式

一个整数，表示小 P 的物流公司完成阶段性工作所需要的最短时间。

输入输出样例

输入 #1

6 3 
1 2 3 
1 6 4 
3 1 7 
4 3 6 
3 5 5 
3 6 
2 5 
4 5

输出 #1

11

说明/提示

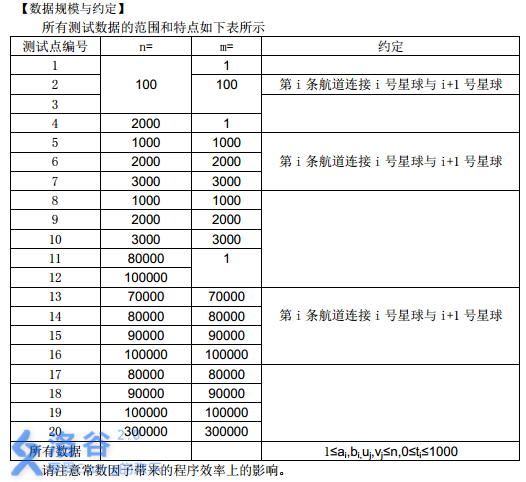
所有测试数据的范围和特点如下表所示

请注意常数因子带来的程序效率上的影响。

对于 100\% 的数据，保证：1≤ai,bi≤n，0≤ti≤1000，1≤ui,vi≤n。

江江强～

正题

抽象题意：一棵有边权的树有n个节点

给出m条路径的起点和终点

你可以任意将一条边的边权变成0

求操作后m条边中所有路径最小权值和的最大值最小是多少

这TM原题不比这说的清楚。。。

但抽象完了后就能想到二分答案力

check怎么做呢？

如果已知路径有边权和 比 二分到的答案大的

if(edge_sum[i]>mid)

那必须删掉这条路径上的一条边。

这种路径有很多，怎么办？

只能删这些路径的交集了！

补充一下交集怎么求，十分滴简单（

只要差分维护区间和，把路径上的边++，最后看哪条边==路径条数就可以了

。。。

只要交集中有一个可以让最长的路径都降到mid一下，那就return true;

//最后吹一下aqx二分

int now=0;//下界
for(int step=(1<<20)/*区间大小*/;step>0;step>>=1){
    if(check(now+step))now+=step;
}

//妈的难死了
//二分答案
//假设二分到的答案以上的都被薄纱了
//那就枚举一遍，O(m)枚举，没办法，只剩O(1)check
// /kk
//O(1)check怎么check
//怎么O(n)以内判断能不能
//check()
/*

首先选的边要大于最大值减去二分值
如何确定这条边在每个的最短路径上

江江强
江江还是强

*/
#include<iostream>
#include<algorithm>
#include<cstring>
#define int long long
using namespace std;
//重构代码
//我要读入一棵前缀树，怎么办
//蚌
//得存边权 /kk
const int MAXN=3e5+10;
struct tree{//前项星罢了
    int to;
    int w;
    int next;
}edge[MAXN*2];
int head[MAXN];
int _cnt=0;
void add(int u,int v,int w){
    edge[++_cnt].to=v;
    edge[_cnt].w=w;
    edge[_cnt].next=head[u];
    head[u]=_cnt;
}
int n,m;
//打个快读
inline int read(){
    int s=0,f=1;
    char c=getchar();
    while(c<48 || c>57){if(c=='-')f=-f;c=getchar();}
    while(c>=48 && c<=57)s=s*10+c-48,c=getchar();
    return s*f;
}
int pretree[MAXN];
int d[MAXN][20];
int depth[MAXN];
void predfs(int x,int dep){//要算根到节点的路径和
    depth[x]=dep;
    for(int i=head[x];i!=0;i=edge[i].next){
        int nxt=edge[i].to;
        if(depth[nxt])continue;
        int w=edge[i].w;
        pretree[nxt]=pretree[x]+w;
        d[nxt][0]=x;
        for(int i=1;i<20;i++){//还要预处理LCA
            d[nxt][i]=d[d[nxt][i-1]][i-1];
        }
        predfs(nxt,dep+1);
    }
}
//还是 亲 爱 的 LCA
int LCA(int u,int v){
    if(depth[u]<depth[v]){
        swap(u,v);
    }
    for(int i=19;i>=0;i--){
        if(depth[d[u][i]]>=depth[v]){
            u=d[u][i];
        }
    }
    if(u==v)return u;
    for(int i=19;i>=0;i--){
        if(d[u][i]!=d[v][i]){
            u=d[u][i];
            v=d[v][i];
        }
    }
    return d[u][0];
}
struct node{
    int s;
    int t;
    int lca;
    int length;
    friend bool operator <(const node &a,const node &b){
        return a.length<b.length;
    }
}ship[MAXN];//从0开始
//大毒瘤来喽
int cnttree[MAXN];
//dfs子树和
//打ABC去了，鸽了鸽了
//开打
void dfs(int x){
    //我前缀都不会写 /kk
    //随便写一个试试
    for(int i=head[x];i!=0;i=edge[i].next){
        int nxt=edge[i].to;
        if(nxt==d[x][0])continue;
        dfs(nxt);
        cnttree[x]+=cnttree[nxt];
    }
    return ;
}
//「难蚌的check」|二分的核心
bool check(int x){
    memset(cnttree,0,sizeof(cnttree));
    //还得差分
    //先得看哪些要差
    //aqx二分！
    //不对lower_bound够了
    int pos=upper_bound(ship,ship+m,(node){0,0,0,x})-ship;//mid以上都要干掉，因为mid要留下，所以要严格大于mid
    if(pos==m)return true;//全保留就不算了
    int left=m-pos;//就剩这点点
    int target=ship[m-1].length-x;
    for(int i=pos;i<m;i++){//左闭右开
        //上边！
        cnttree[ship[i].s]++;
        cnttree[ship[i].t]++;
        cnttree[ship[i].lca]-=2;
    }
    dfs(1);
    for(int i=1;i<=n;i++){
        if(cnttree[i]==left && pretree[i]-pretree[d[i][0]]>=target)return true;
    }
    return false;
}
signed main(){
    n=read(),m=read();
    int u,v,w;
    for(int i=1;i<n;i++){
        u=read(),v=read(),w=read();
        add(u,v,w);
        add(v,u,w);
    }
    predfs(1,1);
    for(int i=0;i<m;i++){
        u=read();
        v=read();
        //妈的不想打lca /fn/fn！
        int lca=LCA(u,v);
        ship[i]=(node){u,v,lca,pretree[u]+pretree[v]-2*pretree[lca]};
    }
    sort(ship,ship+m);
    //突然没思路了 o(0_0')o
    //等等我想想排序的细节
    //就是，咋做来着
    //二分的时候
    //再二分一次找到哪些边的length比mid长
    //——这就是要干掉的边
    //O(m)处理每条路径的差分加减
    //O(n)dfs一遍得到原数组
    //O(n)处理每条==cnt的边，要是边长>=最长边-mid就是true
    //问题不大
    //二分喽～
    //aqx 二分！
    int now=0;//问的是删一条边 最长 路径的 最 小 值 
    if(check(0)){//特判注意！！！
        cout<<'0';//当然还有奇迹淫巧 ： now=-1初值
        return 0;
    }
    for(int i=(1<<29);i>0;i>>=1){
        if(!check(i+now)){//最后一个不行的
            now+=i;
        }
    }   
    cout<<now+1;
    return 0;//完结撒花！～
}