软件包管理器|P2146
https://www.luogu.com.cn/problem/P2146
题目背景
Linux 用户和 OSX 用户一定对软件包管理器不会陌生。通过软件包管理器,你可以通过一行命令安装某一个软件包,然后软件包管理器会帮助你从软件源下载软件包,同时自动解决所有的依赖(即下载安装这个软件包的安装所依赖的其它软件包),完成所有的配置。Debian/Ubuntu 使用的 apt-get,Fedora/CentOS 使用的 yum,以及 OSX 下可用的 homebrew 都是优秀的软件包管理器。
题目描述
你决定设计你自己的软件包管理器。不可避免地,你要解决软件包之间的依赖问题。如果软件包 a 依赖软件包 b,那么安装软件包 a 以前,必须先安装软件包 b。同时,如果想要卸载软件包 b,则必须卸载软件包 a。
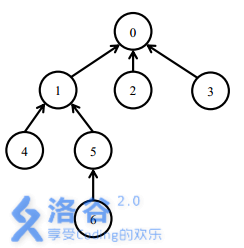
现在你已经获得了所有的软件包之间的依赖关系。而且,由于你之前的工作,除 0 号软件包以外,在你的管理器当中的软件包都会依赖一个且仅一个软件包,而 0 号软件包不依赖任何一个软件包。且依赖关系不存在环(即不会存在 m 个软件包 a1,a2,…,am,对于 i\<mi,ai依赖 ai+1,而 am 依赖 a1 的情况)。
现在你要为你的软件包管理器写一个依赖解决程序。根据反馈,用户希望在安装和卸载某个软件包时,快速地知道这个操作实际上会改变多少个软件包的安装状态(即安装操作会安装多少个未安装的软件包,或卸载操作会卸载多少个已安装的软件包),你的任务就是实现这个部分。
注意,安装一个已安装的软件包,或卸载一个未安装的软件包,都不会改变任何软件包的安装状态,即在此情况下,改变安装状态的软件包数为 0。
输入格式
第一行一个正整数 n,表示软件包个数,从 0 开始编号。
第二行有 n−1 个整数,第 i 个表示 i 号软件包依赖的软件包编号。
然后一行一个正整数 q,表示操作个数,格式如下:
install x表示安装 x 号软件包uninstall x表示卸载 x 号软件包
一开始所有软件包都是未安装的。
对于每个操作,你需要输出这步操作会改变多少个软件包的安装状态,随后应用这个操作(即改变你维护的安装状态)。
输出格式
输出 q 行,每行一个整数,表示每次询问的答案。
输入输出样例
输入 #1
7
0 0 0 1 1 5
5
install 5
install 6
uninstall 1
install 4
uninstall 0输出 #1
3
1
3
2
3输入 #2
10
0 1 2 1 3 0 0 3 2
10
install 0
install 3
uninstall 2
install 7
install 5
install 9
uninstall 9
install 4
install 1
install 9输出 #2
1
3
2
1
3
1
1
1
0
1说明/提示
安装 5 号软件包,需要安装 0,1,5 三个软件包。
之后安装 6 号软件包,只需要安装 6 号软件包。此时安装了 0,1,5,6 四个软件包。
卸载 1 号软件包需要卸载 1,5,6 三个软件包。此时只有 0 号软件包还处于安装状态。
之后安装 4 号软件包,需要安装 1,4 两个软件包。此时 0,1,4 处在安装状态。最后,卸载 0 号软件包会卸载所有的软件包。
思路
这道题近于模板,题意极其清楚:
要么加条链,要么删棵子树
首先子树,这个简单,因为一棵子树的dfs序是连续的
浅证一下:dfs中,由于回溯法,从某个节点回溯出来后就不可能在进去访问其子树了,为了全部遍历,那第一次访问到时就会将其访问完,故是连续的
所以删子树在线段树上维护不难
然后就是加链。
实践会发现,加链慢的地方在于要一个一个往上找,dfs序不完全连续,不能直接在线段树上区间修改。
但是我们发现当节点是独生子并且他只有一个儿子时,dfs序是连续的
说明一条短链的dfs序总是连续的(定义短链为不蔓不枝者)
我们还发现一些短链可以连成dfs序连续的长链
每当我们有一条dfs序连续的链,我们就可以在线段树上logn处理
要是链越长,链就越少(雾
要是某个点跳到了一条长链上,它就可以飞快的完成一段距离
所以我们希望长链尽量多的惠及更多点
于是dfs时加入贪心策略,优先走子树和更大的儿子,这样这一段长链的dfs序就是连续的了。
哇,树剖讲完了
(没图,好难讲。。)
cky注: 现在能放图了直接上传
当我们剖好树后,我们每次都往树上加一段剖出来的链就能很快的完成加链了,这样一直加到根节点
#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<stack>
#include<cmath>
using namespace std;
const int MAXN=1e5+10;
int n,m;
inline int read(){
int s=0,f=1;
char c=getchar();
while(c<'0' || c>'9'){if(c=='-')f=-f;c=getchar();}
while(c>='0' && c<='9')s=s*10+c-'0',c=getchar();
return s*f;
}
//前项星!!!
int a[MAXN];
int head[MAXN];
int cnt=0;
struct graph{
int to,next;
}edge[MAXN];
void add(int u,int v){
edge[cnt].to=v;
edge[cnt].next=head[u];
head[u]=cnt++;
}
//剖树了
//还要打一棵线段树 /kk
int dfn[MAXN];
int s[MAXN];
int depth[MAXN];
int f[MAXN];
int h[MAXN];
int ma[MAXN];
void predfs(int x,int dep,int fa){
depth[x]=dep;
f[x]=fa;
s[x]=1;
for(int i=head[x];i!=-1;i=edge[i].next){
int nxt=edge[i].to;
//我单向存边根本不怕
//if(depth[nxt])continue;
predfs(nxt,dep+1,x);
s[x]+=s[nxt];
}
}
//树剖!
int cnt2=0;
void dfs(int x,int fa){
dfn[x]=++cnt2;
h[x]=fa;
ma[x]=dfn[x];
int maxsum=0;
int maxson=0;
for(int i=head[x];i!=-1;i=edge[i].next){
int nxt=edge[i].to;
//if(dfn[nxt])continue;
if(s[nxt]>maxsum){
maxson=nxt;
maxsum=s[nxt];
}
}
if(maxsum==0)return;
dfs(maxson,fa);
ma[x]=max(ma[x],ma[maxson]);
for(int i=head[x];i!=-1;i=edge[i].next){
int nxt=edge[i].to;
if(dfn[nxt])continue;
dfs(nxt,nxt);
ma[x]=max(ma[x],ma[nxt]);
}
return;
}
//。。。。。。打线段树!!!!
int tree[MAXN*4];
int lazy[MAXN*4];
#define pushup(x) tree[x]=tree[ls(x)]+tree[rs(x)]
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define mid ((l+r)>>1)
#define int long long
void pushdown(int x,int len){//难受的,lazy要想好,这里空值为-1要注意
if(lazy[x]==-1)return;
lazy[ls(x)]=lazy[x];
lazy[rs(x)]=lazy[x];
tree[ls(x)]=lazy[x]*(len-(len>>1));
tree[rs(x)]=lazy[x]*(len>>1);
lazy[x]=-1;
}
void modify(int l,int r,int L,int R,int x,int v){
if(l>=L && r<=R){
lazy[x]=v;
tree[x]=v*(r-l+1);
return ;
}
if(l>R || r<L)return;
pushdown(x,r-l+1);
modify(l,mid,L,R,ls(x),v),modify(mid+1,r,L,R,rs(x),v);
pushup(x);
return;
}
int query(int l,int r,int L,int R,int x){
if(l>=L && r<=R)return tree[x];
if(l>R || r<L)return 0;
pushdown(x,r-l+1);
return query(l,mid,L,R,ls(x))+query(mid+1,r,L,R,rs(x));
}
#define lowbit(x) ((x)&(-(x)))
void print(int x,int dep){//这个debug有大用
if(dep>4)return;
for(int i=log(x)/log(2)-1;i>=0;i--){
cout<<'\t';
if(((1<<i)|x)!=x){
cout<<'|';
}
}
if(x&1)cout<<'!';
cout<<"-----"<<x<<':'<<tree[x]<<','<<lazy[x]<<endl;
print(ls(x),dep+1),print(rs(x),dep+1);
}
signed main(){
memset(head,-1,sizeof(head));
memset(lazy,-1,sizeof(lazy));
n=read();
int u;
for(int i=1;i<n;i++){
u=read();
add(u,i);
}
predfs(0,1,-1);
dfs(0,0);
m=read();
string tmp;
int x;
for(int i=0;i<m;i++){
cin>>tmp>>x;
if(tmp=="install"){
int pre=query(1,n,1,n,1);
while(x!=-1){
modify(1,n,dfn[h[x]],dfn[x],1,1);
x=f[h[x]];
}
cout<<query(1,n,1,n,1)-pre<<endl;
}
else{
int pre=query(1,n,1,n,1);
modify(1,n,dfn[x],ma[x],1,0);
cout<<pre-query(1,n,1,n,1)<<endl;
}
}
return 0;
}