更为厉害|P3899
https://www.luogu.com.cn/problem/P3899
题目描述
设 T 为一棵有根树,我们做如下的定义:
- 设 a 和 b 为 T 中的两个不同节点。如果 a 是 b 的祖先,那么称“a 比 b 更为厉害”。
- 设 a 和 b 为 T 中的两个不同节点。如果 a 与 b 在树上的距离不超过某个给定常数 x,那么称“ a 与 b 彼此彼此”。
给定一棵 n 个节点的有根树 T,节点的编号为 1 到 n,根节点为 1 号节点。 你需要回答 q 个询问,询问给定两个整数 p 和 k,问有多少个有序三元组 (a,b,c) 满足:
- a,b,c 为 T 中三个不同的点,且 a 为 p 号节点;
- a 和 b 都比 c 更为厉害;
- a 和 b 彼此彼此。这里彼此彼此中的常数为给定的 k。
输入格式
输入文件的第一行含有两个正整数 n 和 q,分别代表有根树的点数与询问的个数。
接下来 n−1 行,每行描述一条树上的边。每行含有两个整数 u 和 v,代表在节点 u 和 v 之间有一条边。
接下来 q 行,每行描述一个操作。第 i 行含有两个整数,分别表示第 i 个询问的 p 和 k。
输出格式
输出 q 行,每行对应一个询问,代表询问的答案。
输入输出样例
输入 #1
5 3
1 2
1 3
2 4
4 5
2 2
4 1
2 3输出 #1
3
1
3说明/提示
样例中的树如下图所示:
对于第一个和第三个询问,合法的三元组有 (2,1,4)、 (2,1,5) 和 (2,4,5)。
对于第二个询问,合法的三元组只有 (4,2,5)。
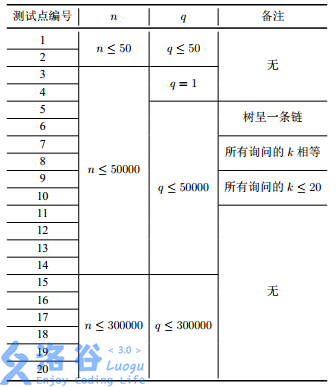
所有测试点的数据规模如下:
对于全部测试数据的所有询问,1≤p,k≤n。
不急,先抽象题意
首先第一步,我们要看题目给的条件有没有什么结论,是不是有很强的限制
设 a 和 b 为 T 中的两个不同节点。如果 a 是 b 的祖先,那么称“a 比 b 更为厉害”。
设 a 和 b 为 T 中的两个不同节点。如果 a 与 b 在树上的距离不超过某个给定常数 x,那么称“ a 与 b 彼此彼此”。
a,b,c 为 T 中三个不同的点,且 a 为 p 号节点;
a 和 b 都比 c 更为厉害;
a 和 b 彼此彼此。这里彼此彼此中的常数为给定的 k。
copy过来方便看
a 和 b 都比 c 更为厉害;
这能说明什么?
c同时要是a和b的子孙。
那a,b一定也是祖孙关系
(这要解释吗。。。)
我也不会
如果一定是祖孙关系,那有个条件就变的简单了:
设 a 和 b 为 T 中的两个不同节点。如果 a 与 b 在树上的距离不超过某个给定常数 x,那么称“ a 与 b 彼此彼此”。
那就是不树上最短路跑LCA了,而是深度差。
于是题变成了:
给一个定点P,深度差不超过k的地方找个b,再在更深的那个节点的子树上取一个点c
取c的情况个数就是子树大小减1,dfs预处理很香;
当b是a的祖先时,a永远是更深的那个,c在它的子树上取,乘法原理即得此时情况数等于b的情况数乘上a子树大小减一;
要是a的深度大于k,那么b能选够k个,否则只有剩余深度那么多。
真正难的来了:当b是a的子孙时,在深度差为k的范围内把每种可能的b的子树和加起来
(上图!!!)
。。又。 隹。。;受。 。 。
这时候,我们如果能拿出一个柿子,那思路就可以继续往下了
$$ \sum_{dep_i \in (dep_p,dep_p+k],dfn_i \in (dfn_p,ma_p] }^{}(s_i-1) = \sum_{i=dep_p}^{dep_p+k}\sum_{j=dfn_p}^{ma_p}is(i,j) \times (s_i-1) $$
(变量看代码)
非常抽象,但是我们发现,我们找到了每个点的两个维度,要求符合两个维度限制的点之和。
于是我们把这些点撒到二维平面上,问题不就——
退化了。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
//艹炸long long了
#define int long long
/*
更为蒟蒻
kaiyi的疑惑 「?·问号·?」
c --> b --> a
*/
//快读读,读快快~
inline int read(){
int s=0,f=1;
char c=getchar();
while(c<48 || c>57){if(c=='-')f=-f;c=getchar();}
while(c>=48 && c<=57)s=s*10+c-48,c=getchar();
return s*f;
}
const int MAXN=3e5+10;
//一棵状数组树是很好吃的
int c[MAXN];
int n,m;
#define lb ((i)&(-(i)))
int query(int x){
if(x==0)return 0;
int ret=0;
for(int i=x;i>0;i-=lb)ret+=c[i];
return ret;
}
void modify(int x,int v){
if(x==0)return;
for(int i=x;i<=n;i+=lb)c[i]+=v;
}
//存树就是存图 ——xky_OI_strong-2021.7 发行版
int head[MAXN];
int _cnt=0;
struct node{
int to;
int next;
}edge[MAXN*2];
void add(int u,int v){
edge[_cnt].to=v;
edge[_cnt].next=head[u];
head[u]=_cnt++;
}
//现在我们要处理子树上有多少节点这个问题
//还有深度
//所以dfs!
int depth[MAXN];
int dfn[MAXN];
int s[MAXN];
int cnt=0;
int ma[MAXN];
void dfs(int x,int dep){
s[x]=1;
dfn[x]=++cnt;
ma[x]=dfn[x];
depth[x]=dep;
for(int i=head[x];i!=-1;i=edge[i].next){
int nxt=edge[i].to;
if(dfn[nxt])continue;
dfs(nxt,dep+1);
ma[x]=max(ma[x],ma[nxt]);
s[x]+=s[nxt];
}
return ;
}
//万事具备,只差二维偏序
/*
(dep,dfn)
dfn作为纵轴
y/dfn
^
|
|
|
|
*------------> x/dep
《 扫 描 线 》
*/
struct pt{int d;int v;};
vector<pt> point[MAXN*2];
struct nb{
int l;
int r;
int o;
bool is_plus;
};
vector <nb> problem[MAXN*2];
int ans[MAXN];
//lovely main func~
signed main(){
memset(head,-1,sizeof(head));
n=read();
m=read();
//init:
int x,y;
int k,p;
for(int i=1;i<n;i++){
x=read(),y=read();
add(x,y),add(y,x);
}
dfs(1,1);//深度为1, 1 1 1~
for(int i=1;i<=n;i++){
point[depth[i]].push_back(pt{dfn[i],s[i]-1});
}
//询问
for(int i=0;i<m;i++){
p=read();
k=read();
/* 处理询问 */
//二维限制 x: dep ∈ ( depth[x] , depth[x]+k ]
//二维限制 y: dfn ∈ ( dfn[x] , ma[x] ]
// --
problem[depth[p]].push_back({dfn[p],ma[p],i,false});
//++
problem[depth[p]+k].push_back({dfn[p],ma[p],i,true});
//细节tm多死
ans[i]=(s[p]-1)*min(depth[p]-1,k);
}
{//<< 扌彐 扌苗 纟戋 >>
for(int i=1;i<=2*n;i++){
for(auto j:point[i]){
modify(j.d,j.v);
}
for(auto j:problem[i]){
if(j.is_plus){
ans[j.o]+=query(j.r)-query(j.l);
}
else{
ans[j.o]-=query(j.r)-query(j.l);
}
}
}
}
//输出喽~
for(int i=0;i<m;i++){
cout<<ans[i]<<endl;
}
return 0;
}